Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
Mit nextGaussian() positive Zahlen erzeugen?
- Themenstarter slitec
- Beginndatum
mihe7
Top Contributor
Das hatte ich erst auch überlegt, aber ändert das nicht die Verteilung? Mein Hirn ist heute schon abgeraucht.abs() ?
httpdigest
Top Contributor
Japp. Wird dann die "Half-normal distribution".aber ändert das nicht die Verteilung?
Ich brauch die Zahlen später für eine Lorenz-Kurve und für den Gini-Koeffizient. Da bekomme ich mit negativen Zahlen Probleme.Was spricht dagegen, so lange Zufallswerte zu erzeugen, bis sie im gewünschten Bereich liegen?
mihe7
Top Contributor
Welchen Bereich? Die Zufallszahlen gehen theoretisch von -infty bis +infty.Was spricht dagegen, den Bereich mit +1 ins Positive zu verschieben?
temi
Top Contributor
Welchen Bereich? Die Zufallszahlen gehen theoretisch von -infty bis +infty.
the next pseudorandom, Gaussian ("normally") distributed double value with mean 0.0 and standard deviation 1.0 from this random number generator's sequence
Ich hatte das so interpretiert, dass der Wertebereich von -1.0 bis + 1.0 geht. Da habe ich mich wohl geirrt.
mihe7
Top Contributor
Das ist ja der Mist 
Man hat einen Erwartungswert und die Standardabweichung. Ca. 69 % der normalverteilten Werte liegen im Bereich des Erwartungswerts +/- Standardabweichung. Verdoppelt man die Standardabweichung, liegen etwa 95 % der Werte in dem sich ergebenden Bereich. Man kann das Intervall aber beliebig groß wählen, man wird nie 100 % erreichen.
Man hat einen Erwartungswert und die Standardabweichung. Ca. 69 % der normalverteilten Werte liegen im Bereich des Erwartungswerts +/- Standardabweichung. Verdoppelt man die Standardabweichung, liegen etwa 95 % der Werte in dem sich ergebenden Bereich. Man kann das Intervall aber beliebig groß wählen, man wird nie 100 % erreichen.
temi
Top Contributor
Man kann das Intervall aber beliebig groß wählen, man wird nie 100 % erreichen.
Mathe war schon immer meine schwache Seite, aber der Bereich kann ja nicht unendlich sein, weil er durch Double sowieso eingeschränkt wird. Da der TO nur positive Zahlen möchte, schränkt er diesen Bereich nochmal ein. Es ist also nur eine Frage der Anwendung, ob es ausreichend ist, wenn er den Erwartungswert in die Mitte des positiven Bereiches verschiebt.
Oder lieg ich da jetzt ganz falsch?
Zuletzt bearbeitet:
mihe7
Top Contributor
Ich könnte mir vorstellen, dass sich ein Verfahren finden lässt, das die in der Praxis geltenden Grenzen ausnutzt. Einfach den Erwartungswert nach Double.MAX_VALUE/2 zu verschieben, funktioniert allerdings nicht: aufgrund der Präzision von double würdest Du (fast) immer den gleichen Wert erhalten, nämlich Double.MAX_VALUE/2.
X
Xyz1
Gast
Moment mal, der Wertebereich ist wirklich nicht [-1.0, +1.0]? Ich hatte das auch so verstanden.Ich hatte das so interpretiert, dass der Wertebereich von -1.0 bis + 1.0 geht.
mihe7
Top Contributor
Java:
import java.util.Random;
public class Gaussian {
public static void main(String[] args) {
Random rand = new Random(1L);
int count = 0;
do {
double value;
do {
value = rand.nextGaussian();
} while (Math.abs(value) <= 1.0);
System.out.println(value);
count++;
} while (count < 10);
}
}liefert
Code:
1.561581040188955
-1.0912278829447088
-1.1182832102556484
-1.6583217791337177
-1.8821643777572246
-1.160868794354026
2.8307323206471837
-1.3604870442090895
-1.1629624729268742
-1.3049338775280348
X
Xyz1
Gast
Dann setzte ich auf das falsche Pferd...
Aber was wäre damit:
Bei
Aber was wäre damit:
Java:
public static double ng(double a, double b) {
double eps = 0.001;
if (!(a + eps < b)) {
throw new IllegalArgumentException("a must be lower than b");
}
Random r = new Random();
double g = r.nextGaussian();
while (g < a || g > b) {
g = r.nextGaussian();
}
return g;
}
public static void main(String[] args) {
for (int i = 0; i < 20; i++) {
System.out.println(ng(0.10, 0.11));
}
}Bei
ng(10, 11) hält es allerdings nicht an...temi
Top Contributor
Aber was wäre damit
Ist das, was am Ende noch übrig bleibt tatsächlich noch eine gaussche Verteilung, wenn deren Erwartungswert bei 0 liegt?
Praktisch gesehen, schneidest du doch ein Stück aus der Verteilungskurve aus.
Sollte aber klappen, den Erwartungswert in die Mitte des gewünschten Intervalls zu "schieben" und die Standardabweichung anzupassen (zB 1/6 der Interfvallgröße). Wenn man alles außerhalb liegende abschneidet, verliert man ein paar Promille (je nach Standardabweichung), aber nutzen lassen sollte es sich trotzdem.
mihe7
Top Contributor
Die Wahrscheinlichkeit, dass Du eine Zufallsvariable > 4,09 erhältst, ist nahezu 0. Siehe https://de.wikipedia.org/wiki/Standardnormalverteilungstabelle.Being(10, 11)hält es allerdings nicht an...
So sehe ich das auch. Wenn man nur eine Seite abschneidet, dürfte sich der Erwartungswert verschieben. Wenn man sich überlegt, dass es fast unmöglich ist, Werte jenseits +/- 5 zu erhalten, spielt das für Erwartungswerte > 5 praktisch keine Rolle.Sollte aber klappen, den Erwartungswert in die Mitte des gewünschten Intervalls zu "schieben" und die Standardabweichung anzupassen (zB 1/6 der Interfvallgröße). Wenn man alles außerhalb liegende abschneidet, verliert man ein paar Promille (je nach Standardabweichung), aber nutzen lassen sollte es sich trotzdem.
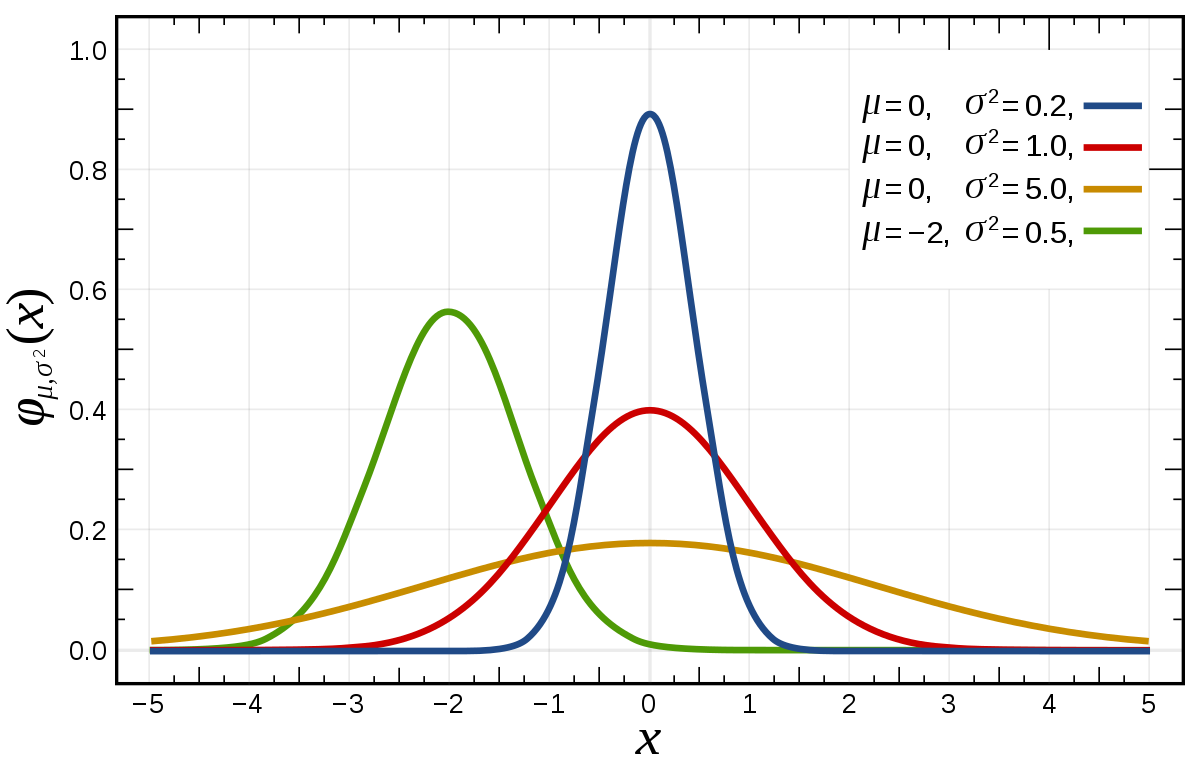
Falls es jemanden interessiert, hier der Octave Code (Achtung: hingerotzt) für den Graphen von oben:
Code:
function retval = incomings(n,m,s)
X=zeros(n,1);
for i = 1:n
do
v = randn()*s+m;
until (v >= 0)
X(i) = round(v);
endfor
retval = X;
endfunction
I=incomings(10000, 1500, 500);
X=sort(I);
total=sum(X)
C=cumsum(X)/total;
Y=[0;accumarray(ceil((1:rows(C)) / 1000)(:), C)];
I=abs(randn(10000,1))*500+1500;
X=sort(I);
total=sum(X)
C=cumsum(X)/total;
Z=[0;accumarray(ceil((1:rows(C)) / 1000)(:), C)];
hf = figure()
hold on
plot(0:0.1:1, Y/max(Y), "markersize", 10, "o-")
plot(0:0.1:1, Z/max(Z), "markersize", 10, "xr-")
hold off
print(hf, "lorenz.png", "-dpng")Wenn ich mich nicht vertan habe, sollte das ein normalverteiltes Zufallseinkommen von 10.000 Personen simulieren mit einem Durchschnittseinkommen von 1.500 €, wobei knapp 70 % im Bereich zwischen 1.000 € und 2.000 € verdienen.
Aber Achtung: ich kenne mich mit dem Zeug echt nicht aus.
Etwa so sollte das klappen:
Java:
import java.util.*;
public class NormalVerteilung {
private final double from;
private final double to;
private final Random random = new Random();
public NormalVerteilung(final double from, final double to) {
this.from = from;
this.to = to;
}
public double next() {
final double expectation = from + (to - from) / 2;
final double stdDev = (to - from) / 6; //knapp 2‰ liegen dann außerhalb, uU anpassen
double result;
do {
result = random.nextGaussian() * stdDev + expectation;
} while (result < from || result > to);
return result;
}
public static void main(String[] args) {
final NormalVerteilung normalVerteilung = new NormalVerteilung(5, 10);
for (int i = 0; i < 1000; i++) {
System.out.println(normalVerteilung.next());
}
}
}mihe7
Top Contributor
Weniger als gar nicht gibt es also doch?!?Ich kenne mich anscheinend noch weniger gut als mihe7 damit aus...
temi
Top Contributor
Etwa so sollte das klappen:
Achtung Mathematik-DAU: Wofür ist nochmal das "stdDev" nötig?
Edit: Ich glaub ich hab es verstanden. Damit wird das Ergebnis auf den gewünschten Bereich "gestreckt", oder?
Zuletzt bearbeitet:
Achtung Mathematik-DAU: Wofür ist nochmal das "stdDev" nötig?
Achtung, auch Mathematik-DAU:
Hier hat @mihe7 den Hintergrund erklärt.
Man hat einen Erwartungswert und die Standardabweichung. Ca. 69 % der normalverteilten Werte liegen im Bereich des Erwartungswerts +/- Standardabweichung. Verdoppelt man die Standardabweichung, liegen etwa 95 % der Werte in dem sich ergebenden Bereich. Man kann das Intervall aber beliebig groß wählen, man wird nie 100 % erreichen.
Will man dann zB, dass 69% aller Werte im Intervall liegen, muss das Intervall zwei Standardabweichungen groß sein (da Mitte und Erwartungswerts +/- Standardabweichung)
Oder andersrum, wenn das Intervall fest ist, müsste die Standardabweichung so gewählt sein, dass sie genau zwei mal in's Intervall passt.
Mit 3 Standardabweichungen hat man über 99,7% der Werte, deshalb sind's oben die 1/6 des Intervalls.
mihe7
Top Contributor
Wenn das hier so weiter geht, können wir ein Mathe-DAU-Forum aufziehen mit dem Untertitel "Wir haben kein Wissen, davon aber besonders viel"Achtung, auch Mathematik-DAU:
X
Xyz1
Gast
SO, ich habe ein bisschen auf Stack Overflow gesucht und diese Frage scheint doch recht "neu". Jedenfalls sind alle Fragen danach fast alle fast komplett "downgevoted"...
Zum Beispiel: https://stackoverflow.com/questions/629798/problem-with-random-nextgaussian
Ich vermute das liegt in der mathematischen Natur der Sache. Rofl...
Zum Beispiel: https://stackoverflow.com/questions/629798/problem-with-random-nextgaussian
Ich vermute das liegt in der mathematischen Natur der Sache. Rofl...
X
Xyz1
Gast
Juhu, fertig 
(Muss ich mir mal in meinem Utility Kasten speichern
Java:
public static double ng(double a, double b) {
double eps = 0.001;
if (!(a + eps < b)) {
throw new IllegalArgumentException("a must be lower than b");
}
double c = -(b - a) / 2;
double d = +(b - a) / 2;
Random r = new Random();
double g = r.nextGaussian();
while (g < c || g > d) {
g = r.nextGaussian();
}
return g + d + a;
}
public static void main(String[] args) {
double d = 0;
for (int i = 0; i < 10000; i++) {
d += ng(0.10, 0.11) / 10000;
}
System.out.println(d);
d = 0;
for (int i = 0; i < 10000; i++) {
d += ng(10, 11) / 10000;
}
System.out.println(d);
d = 0;
for (int i = 0; i < 10000; i++) {
d += ng(-11, -10) / 10000;
}
System.out.println(d);
}
Code:
0.10501...
10.502...
-10.497...(Muss ich mir mal in meinem Utility Kasten speichern
Ist allerdings je nach Intervall nicht mehr als Normalverteilung erkennbar, da immer eine Standardabweichung von 1Juhu, fertig
Da ist keine Abweichung um 1
https://docs.oracle.com/javase/8/docs/api/java/util/Random.html#nextGaussian() hat gesagt.:Returns the next pseudorandom, Gaussian ("normally") distributed double value with mean 0.0 and standard deviation 1.0 from this random number generator's sequence.
mihe7
Top Contributor
Wie das?Mit einem 0.5-Faktor ist der weg.
X
Xyz1
Gast
Hm , ich weiß nicht was er mit Verschiebung um 1 meint.Wie das?
mihe7
Top Contributor
Er meint, dass nextGaussian() einen Zufallswert mit einer Standardabweichung von 1 (um den Wert 0 herum) liefert. Deine Methode macht zwei Dinge: erstens den Erwartungswert in die Mitte des Intervalls verschieben, zweitens nur Werte innerhalb des Intervalls zurückgeben. Wenn Du also z. B. ein Intervall von [0, 20] angibst, werden sich die Zufallswerte mit ebenfalls ca. 70 % im Intervall [9, 11] bewegen.
X
Xyz1
Gast
X
Xyz1
Gast
Ok, das ist Intervallabhängig. Zum Beispiel wählt man -5 bis +5:
Das entspricht fast schon dieser Normalverteilung...
Möchte man das nicht, könnte man die Werte doch "strecken" (also auseinander-ziehen) mithilfe diese "Streckungsfaktors"?
Java:
double[] d = new double[11];
for (int i = 0; i < 1000; i++) {
int e = (int) Math.round(ng(-5, +5)) + 5;
d[e] += 1.0 / 1000.0;
}
for (int i = 0; i < d.length; i++) {
double e = d[i];
System.out.println(((i - 5) + " " + (e)));
}
Code:
-5 0.0
-4 0.001
-3 0.009 (Nullen entfernt)
-2 0.067
-1 0.237
0 0.379
1 0.231
2 0.073
3 0.003
4 0.0
5 0.0Das entspricht fast schon dieser Normalverteilung...
Möchte man das nicht, könnte man die Werte doch "strecken" (also auseinander-ziehen) mithilfe diese "Streckungsfaktors"?
Das hab ich nicht in Zweifel gezogenDas entspricht fast schon dieser Normalverteilung...
Aber nimm zb mal 0-1 (und skalier das für die Ausgabe auf 0-10), dann sieht man, was ich meine. Oder alternativ 0-100 (und skaliert auf 0-10).
Das soll keineswegs heißen, dass es falsch ist - man muss es nur wissen und beachten.
Je nach Anwendungsfall macht das eben Probleme.
Ähnliche Java Themen
Ähnliche Java Themen
-
Erste Schritte nextGaussian zwischen zwei Werten
- Gestartet von ungenau
- Antworten: 19
-
-
-
Positive und negative Zahlen mit Regex extrahieren
- Gestartet von Caliburns
- Antworten: 8
-
-
Wie ziehe ich positive ungerade Zahlen von meinem Hauptwert ab?
- Gestartet von Wasserranzen
- Antworten: 17
-
Greates Commong Dividend - euklidischer Algorithmus, modulos not positive
- Gestartet von Lukases2
- Antworten: 5
-
Operatoren Der Tide Operator und positive Ganzzahlen in Binär
- Gestartet von ubaro1
- Antworten: 1
-
Input/Output Positive und negative Zahlen ausgeben
- Gestartet von BartMarley
- Antworten: 27
-
Simple Frage: Positive Zahlen zu Negativen machen.
- Gestartet von joni89
- Antworten: 11
-
-
G
-
-
-
Anzahl Random Zahlen mit Scanner abfragen und in Array speichern
- Gestartet von onlyxlia
- Antworten: 10
-
Java Array - Buchstaben als Zahlen ausgeben
- Gestartet von überlebender
- Antworten: 22
-
Aus Text Datei nur Zahlen übernehmen
- Gestartet von pentilisea
- Antworten: 13
-
Warum werden immer noch doppelte Zahlen ausgegeben ?
- Gestartet von Käsekuchen
- Antworten: 13
-
-
-
-
Taschenrechner mit mehr als 2 Zahlen.
- Gestartet von Johannes73
- Antworten: 18
-
Zahlen aus einem char-array per char + Zeichen addieren
- Gestartet von OliI.
- Antworten: 2
-
Alle Zahlen finden, die 3 bestimmte Ziffern enthalten?
- Gestartet von berndoa
- Antworten: 9
-
-
aus 2 random zahlen soll nur die ungerade summe der beiden genommen werden.
- Gestartet von ijsnf
- Antworten: 13
-
-
Threads Counter mit ungeraden Zahlen
- Gestartet von BodyLAB
- Antworten: 32
-
Java 2 Zufalls zahlen generieren.
- Gestartet von JavaBeginner22
- Antworten: 11
-
Wie kann man ein Regex erstellen, die 8-Bit-Binär-Zahlen darstellen.
- Gestartet von Xalo
- Antworten: 1
-
Stream mit den ersten n natürlichen Zahlen
- Gestartet von Mariexshhx
- Antworten: 4
-
Größtes Palindrom Produkt aus zwei dreistelligen Zahlen
- Gestartet von DrPils
- Antworten: 60
-
Methode, die prüft ob in einem Int-Array maximal 2 Zahlen enthalten sind, die größer als ihr Vorgänger sind
- Gestartet von TuffKultur
- Antworten: 5
-
-
Verzweigungen zahlen multiplizieren
- Gestartet von AhmadSlack
- Antworten: 4
-
Array Multiplikation der ersten n Zahlen
- Gestartet von padde479
- Antworten: 7
-
-
Wie würde man einen regulären Ausdruck in Java schreiben, der prüft, dass zwei bestimtme Zahlen nicht nebeneinadner sind?
- Gestartet von berserkerdq2
- Antworten: 3
-
Arrays: Größten Zahlen Unterschied herausfinden
- Gestartet von Hermänchen223
- Antworten: 20
-
Programmieren eines Bots für Zahlen-Brettspiel
- Gestartet von bluetrix
- Antworten: 9
-
Zahlen bis zu einem bestimmten Grenzwert ausgeben
- Gestartet von juliuspilatus
- Antworten: 11
-
Objektorientiertes Programmieren mit Vererbung (Zahlen in Array verschwinden)
- Gestartet von 00111010101
- Antworten: 3
-
Zweidimensionales Array als Tabelle mit befüllten Zahlen
- Gestartet von Peter992
- Antworten: 10
-
Wie ziehe ich von einer bestimmten Zahl, Zahlen ab, bis mein Ergebnis null beträgt?
- Gestartet von Wasserranzen
- Antworten: 10
-
Erste Schritte NullPointerException, Array mit zufälligen Zahlen füllen
- Gestartet von emx-zee
- Antworten: 2
-
Bestimmte Zahlen bei Math.random ausschließen?
- Gestartet von Wuast
- Antworten: 31
-
KErste Schritte "Taschenrechner" zeigt keine Komma Zahlen an.
- Gestartet von Kleechen
- Antworten: 8
-
Drei Zahlen eines Würfelspiels auswerten
- Gestartet von prog6d
- Antworten: 7
-
-
Zahlen rekursiv zerlegen und Ziffern addieren
- Gestartet von sashady
- Antworten: 38
-
-
Teilerfremde Zahlen ausgeben + Zahlenausgabe speichern
- Gestartet von ansystin
- Antworten: 3
-
Häufigkeit einzelner Zahlen in einem Array
- Gestartet von BS1503
- Antworten: 6
-
Programm für die Summer der Zahlen 1- 1ß
- Gestartet von nevel
- Antworten: 12
-
Fibonacci Zahlen rekursiv und iterativ
- Gestartet von jhCDtGVjcZGcfzug
- Antworten: 21
-
Eingegebene Zahlen mit Array ausgeben
- Gestartet von Hallo1234
- Antworten: 18
-
12 Spalten von jeweils 30 Zahlen in Konsole ausgeben
- Gestartet von IlikeJava
- Antworten: 6
-
Array mit Unter- und Obergrenze ganze Zahlen dazwischen erscheinen nicht
- Gestartet von rantonica
- Antworten: 1
-
For Schleife von 1-50 die Zahlen werden durch ein Komma getrennt
- Gestartet von OZAN86
- Antworten: 10
-
Operatoren Alle Zahlen einer ArrayList die durch 5 teilbar ist
- Gestartet von Bademeister007
- Antworten: 2
-
dafür sorgen, dass im JTextfield nur zahlen eingebbar sind
- Gestartet von mhmt_03
- Antworten: 9
-
-
Wie kann ich die Zahlen dieses Arrays dividieren?
- Gestartet von Prometheus1999
- Antworten: 2
-
Nutzer entscheiden lassen, wie viele Zahlen dieser in ein Array eingeben möchte.
- Gestartet von Prometheus1999
- Antworten: 6
-
Bestimmte Zahlen ausgeben mit einer whilfe Schleife
- Gestartet von tetsu
- Antworten: 21
-
Alle Geraden zahlen bis 10 ausgeben
- Gestartet von hallo11
- Antworten: 11
-
Liste mit zufälligen zahlen füllen
- Gestartet von java3690
- Antworten: 27
-
Rekursive String Methode, Gerade Zahlen rausfiltern
- Gestartet von macle
- Antworten: 10
-
Regex nur Zahlen und Punkt zulassen, Keine Eingabe(Leeres TextFeld) nicht zulassen
- Gestartet von MasterShredder
- Antworten: 6
-
-
-
Zahlen werden falsch gekürzt :?
- Gestartet von doubleflip
- Antworten: 27
-
Ungerade Zahlen ausgeben von 1 bis 1000
- Gestartet von HWS_Jung
- Antworten: 8
-
Wörter und Zahlen nach speziellen Wörtern ausgeben
- Gestartet von Noccctis
- Antworten: 11
-
Komplexe Zahlen auf verschiedene Weise addieren
- Gestartet von fusenoepsi
- Antworten: 18
-
Java Int-Array, Zahlen sortieren
- Gestartet von littlebigplanet
- Antworten: 8
-
Fibonacci Zahlen dynamische Programmierung
- Gestartet von baker333
- Antworten: 7
-
Erste Schritte Taschenrechner mit beliebig vielen Zahlen
- Gestartet von vulturas
- Antworten: 5
-
Wie kann ich Zahlen in einzelne Zifferne zerlegen?
- Gestartet von Xalo
- Antworten: 3
-
Rechtsbündige Ausgabe von Zahlen
- Gestartet von Kaktusfan123
- Antworten: 6
-
Wie zwei zahlen in einer Variable speichern?
- Gestartet von AmadeusBot
- Antworten: 7
-
-
Zahlen von einem Array mit zahlen von zweitem Array vergleichen
- Gestartet von eduwei1
- Antworten: 27
-
-
Warum berechnet mein Primzahlenprog zu hohe Zahlen nicht?
- Gestartet von mancko
- Antworten: 20
-
-
-
Fehler bei Zufallsgeneration von Zahlen
- Gestartet von der_Schokomuffin
- Antworten: 7
-
Erste Schritte Alle möglichen ausgaben von 5 Zahlen als Vector
- Gestartet von java_N00B
- Antworten: 7
-
Abstand zum Durchschnitt von 5 Zahlen berechnen...
- Gestartet von Funktionierdochmal
- Antworten: 16
-
Klassen Array Zahlen zu Sternchen (U-Helmich 7.1-4)
- Gestartet von Moji
- Antworten: 5
-
Summe aller echten Teiler und Zahlen zurückgeben
- Gestartet von Funktionierdochmal
- Antworten: 1
-
-
Zahlen im Feld sortieren + Unterprogramm
- Gestartet von Funktionierdochmal
- Antworten: 4
-
-
-
-
-
-
Schlüsselworte Zählen und Zuweisen von eingelesenen Zahlen
- Gestartet von PCFLO
- Antworten: 1
Aktuelle Jobs
-
Wafios Softwareentwickler Cloud (JAVA/Spring) m/w/d - Reutlingen
- Gestartet von Java_Jobs
- Antworten: 0
-
Inek Senior Java Softwareentwickler (m/w/d) - Siegburg
- Gestartet von Java_Jobs
- Antworten: 0
-
Atos Senior Java Architekt (m/w/d) - Fürth
- Gestartet von Java_Jobs
- Antworten: 0
-
-
FCA Bank Java-Entwickler (m/w/d) (Heilbronn)
- Gestartet von Java_Jobs
- Antworten: 0
Neue Themen
-
Wie arbeitet ihr Dokumentationen durch ?
- Gestartet von Narretei
- Antworten: 5
-
Zwei Mal dieselbe Anwendung in 2 verschiedenen Browsern starten
- Gestartet von Anfaengerin
- Antworten: 9
-
Lokaler Entwicklungsserver
- Gestartet von DaBe1812
- Antworten: 11
-
ArraList Objekt mit JButton anzeigen lassen
- Gestartet von Javaman91
- Antworten: 4
-
Fehler bei PUT und POST bei RestTemplate
- Gestartet von krgewb
- Antworten: 1