Erste Schritte Pi Berechnung

[Vladyslav]

Guten Tag,
bitte um Hilfe.
Ich soll hier PI mithilfe von einer Kreiszerlegung berechnet werden.

double r = 1.0;
double h1= 1.0;
double h2;
int teilung; // Wie oft der viertel Kreis zerglegt werden soll
double x = 0.0;
double ausgabe = 0.0;
Scanner scanner = new Scanner (System.in);

System.out.println("Wie oft soll der Viertelkreis zerlegt \nwerden um Pi herauszufinden?");
teilung = scanner.nextInt();

for ( int i = 1; i < teilung; i++)
{
r = r / teilung;

ausgabe = h1 * r;

x = ausgabe;

h2= Math.sqrt(1-Math.pow(r,2)); // Problem wie komme ich auf die verschiedenen höhen ?
ausgabe = h2 * r;

x = (x+ausgabe) * 4;
}
System.out.println(x);

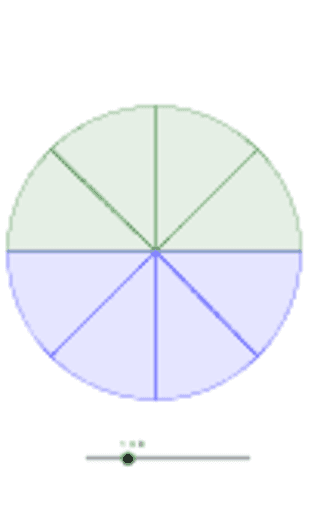
Mein Code dazu. Der Kreis wird in vier viertel geteilt, und ein einzelnes Viertel wird in Rechtecke unterteilt. Je mehr Rechtecke, desto näher ist man an Pi. Am Schluss nimmt man das Ergebnis *4 und dann sollte eine Näherung rauskommen.

Mein Problem ist, mit zwei recht Rechtecken komme ich zurecht. Bei mehr scheitere ich. Je mehr Rechtecke dazu kommen umso weniger wird h2 bei jedem einzelnen.
Könnt mir jemand auf die Sprünge helfen und mir ein hint geben und sagen wie ich es schaffe, dass ich die unterschiedlichen h2 rausbekomme?

mfG !

 

[Xyz1]

Darf Sinus benutzt werden?

		for (int teile = 4; teile <= 50; teile += 2) {
			double w = 360.0 / teile;
			double a = 0.5 * Math.sin(Math.toRadians(w));
			double A = teile * a;
			System.out.println(teile + " " + A);
		}
		System.out.println(Math.PI);

 

[krgewb]

Bitter immer in code-Tags posten.

double r = 1.0;
double h1= 1.0;
double h2;
int teilung; // Wie oft der viertel Kreis zerglegt werden soll
double x = 0.0;
double ausgabe = 0.0;
Scanner scanner = new Scanner (System.in);

System.out.println("Wie oft soll der Viertelkreis zerlegt \nwerden um Pi herauszufinden?");
teilung = scanner.nextInt();

for ( int i = 1; i < teilung; i++)
{
    r = r / teilung;

    ausgabe = h1 * r;

    x = ausgabe;

    h2= Math.sqrt(1-Math.pow(r,2)); // Problem wie komme ich auf die verschiedenen höhen ?
    ausgabe = h2 * r;

    x = (x+ausgabe) * 4;
}
System.out.println(x);

 

[Vladyslav]

@ krgewb sry bin neu in der Materie. Was genau meinst du damit ?

@ Tobias-NRW denke schon, jedoch ist bei mir die Aufgabenstellung die, dass es mithilfe von Rechtseckszerlegung funktionieren soll.

 

[temi]

Was genau meinst du damit ?

Code-Tags: Damit der Code schön formatiert und lesbar angezeigt wird. Klick auf die drei Punkte, rechts vom Smiley und wähle dann Code - Java aus.

 

[Vladyslav]

    public static void main (String [] args )
    {
        double r = 1.0;
        double h1= 1.0;
        double h2;
        int teilung; // Wie oft der viertel Kreis zerglegt werden soll
        double x = 0.0;
        double ausgabe = 0.0;
        Scanner scanner = new Scanner (System.in);
       
        System.out.println("Wie oft soll der Viertelkreis zerlegt \nwerden um Pi herauszufinden?");
        teilung = scanner.nextInt();
       
        for ( int i = 1; i < teilung; i++)
        {
            r = r / teilung;
           
            ausgabe = h1 * r;
           
            x = ausgabe;
           
            h2= Math.sqrt(1-Math.pow(r,2)); // Problem wie komme ich auf die verschiedenen höhen ?
            ausgabe = h2 * r;
           
            x = (x+ausgabe) * 4;
        }
        System.out.println(x);
       
       
       
    }

 

[Xyz1]

Mein Gott, so schwer kann das doch nicht sein, liest eigentlich jemand meine Signatur mal?

Und zu Deinem Problem, ich habe keine Ahnung, wie was "zerlegt" werden soll. Ich habe es in Dreiecke zerlegt, wenn das falsch ist, muss Dir jemand anderes helfen.

 

[kneitzel]

Ich habe mich da heute früh auch etwas mit beschäftigt und ich war mir auch nicht ganz klar darüber, die da denn genau vorgegangen werden soll.

Wenn ich das aber richtig verstanden habe, dann ist die Zerlegung in Dreiecke ja doch das, was er auch (indirekt) haben möchte, denn 2 deiner Dreiecke müssten doch sein Rechteck sein. Da ja eben die Diagonale bekannt ist, sowie ein Winkel bei bei der diagonalen, ist die Berechnung des Rechtecks über so ein Dreieck möglich.

Aber ich kann mich jetzt auch irren. Denn wenn das r bei dem TE der radius ist, dann ist der radius nicht konstant 1? Aber hier denke ich mal ist das auch einfach nur ein typisches Beispiel von "ins eigene Bein geschossen, weil keine vernünftigen Namen vergeben".

==> Mach Dir eine genaue Skizze, auf der aufgezeichnet ist, wie dein Vorgehen aussieht. Da trägst Du dann auch ein, was bekannt ist und was der Wert ist, der Dich interessiert. Dann wird alles sauber benannt und dann kann man Berechnungen auch nachvollziehen. Und so skizzen kann man z.B. mit dem Smartphone abfotografieren und online stellen. Also ist das teilen von so Skizzen auch kein Thema.

Stilistische Mittel wie sinnvoller Einsatz von Farben und so ist noch nicht einmal gefordert ....

 

[mihe7]

Verstehe ich hier was falsch oder ist die Sache im Prinzip sehr einfach? Man hat n Streifen der Breite r/n. Die Höhe ergibt sich aus r² = x² + y², also y(x) = sqrt(r²-x²) für alle x = k*r/n mit k=0,1,...,n-1. Flächen berechnen, aufsummieren, Thema erledigt.

 

[M.L.]

Das könnte beim Thema helfen: https://www.matheretter.de/wiki/herleitung-pi (obwohl man eher an die Monte-Carlo-Simulation denken würde: https://de.wikipedia.org/wiki/Monte-Carlo-Simulation )

 

[mihe7]

Das könnte beim Thema helfen: https://www.matheretter.de/wiki/herleitung-pi (obwohl man eher an die Monte-Carlo-Simulation denken würde: https://de.wikipedia.org/wiki/Monte-Carlo-Simulation )

Ich denke eher ans Integrieren

 

[Xyz1]

Das könnte beim Thema helfen: https://www.matheretter.de/wiki/herleitung-pi

Hä? "Die" verwenden doch auch den Sinus. Ich verstehs nicht.

 

[Xyz1]

enn ich das aber richtig verstanden habe, dann ist die Zerlegung in Dreiecke ja doch das, was er auch (indirekt) haben möchte, denn 2 deiner Dreiecke müssten doch sein Rechteck sein.

Das habe ich auch verstanden. Aber um eine Hälfte des Rechtecks zu erhalten, also genau 1 Dreieck, brauche ich doch wieder den Sinus... (und nicht sqrt und pow) Vielleicht bin ich heute auch einfach zu doof dafür.

 

[kneitzel]

Das habe ich auch verstanden. Aber um eine Hälfte des Rechtecks zu erhalten, also genau 1 Dreieck, brauche ich doch wieder den Sinus... (und nicht sqrt und pow) Vielleicht bin ich heute auch einfach zu doof dafür.

Ja, vollkommen klar. Denn man hat halt nur die Diagonale und 2 Winkel (einer halt ein rechter Winkel). Und da geht die Berechnung nur über sin / cos.

Daran kann ich mich noch sehr gut erinnern - das war damals 8. Klasse und ich habe das dann sogar als Programm geschrieben, das das Dreieck berechnet und dann gezeichnet hat. (Was eine ganz schöne Arbeit war. Auf dem Monitor senkrechte und Waagerechte Linien gemalt und ausgemessen (Monitor damals war ja kein gerade TFT wie heute sondern eine gebogene Röhre ...) und das dann auch auf dem guten alten Nadeldrucker .... Die Seiten des Dreiecks mussten ja exakt richtig gezeichnet sein. Und das Zeichnen ging ja manuell mit Zirkel, d.h. ich habe dann auch die "Kreisabschnitte" gezeichnet - was aber dann natürlich bei mit Ellipsen sein mussten ... Unterschiedliche Anzahl Pixel in x und y Richtung pro cm.

 

[Meniskusschaden]

Darf Sinus benutzt werden?

Falls Sinus erlaubt ist, wird System.out.println(Math.acos(-1)); wohl auch als Lösung akzeptiert werden. Aber warum dann nicht gleich System.out.println(Math.PI);?

 

[mihe7]

Was habt Ihr alle mit Eurem Sinus?

Verstehe ich hier was falsch oder ist die Sache im Prinzip sehr einfach? Man hat n Streifen der Breite r/n. Die Höhe ergibt sich aus r² = x² + y², also y(x) = sqrt(r²-x²) für alle x = k*r/n mit k=0,1,...,n-1. Flächen berechnen, aufsummieren, Thema erledigt.

 

[Meniskusschaden]

Was habt Ihr alle mit Eurem Sinus?

Sehe ich auch so. Pythagoras sollte reichen.

 

[kneitzel]

Wie berechnest du denn da dann das Rechteck? Das ist ja der Grund, wieso ich da eine Skizze einfordere.

Ich gehe bisher von so etwas aus.

Gezeigt wird ein 1/4 Kreis. Der wurde weiter unterteilt und man hat dann halt so ein Dreieck.
Vom Dreieck wissen wir:
- wir haben den Radius
- Wir haben den rechten Winkel
- Wir haben den Winkel, der da grün eingemalt wurde. (Unterteile ich den Kreis in 36 solcher Kuchenstücke, dann sind das 360°/36 = 10°

Die roten Linien haben wir nicht, aber diese lassen sich natürlich berechnen. Einmal ist es radius * sin(alpha) und einmal radius * cos(alpha). Wobei für den Umfang nur das erste gebraucht wird.

Das ist vermutlich etwas, das auch Tobias im Auge hatte weil er dachte, dass dieses kurze rote Stück das ist, was der TE haben will.

Also nun meine Frage: Über was redet ihr genau? Wieso braucht ihr den Sinius nicht?

 

[kneitzel]

Falls Sinus erlaubt ist, wird System.out.println(Math.acos(-1)); wohl auch als Lösung akzeptiert werden. Aber warum dann nicht gleich System.out.println(Math.PI);?

Für die Berechnung des Sinus mit einer bestimmten Genauigkeit benötigt man aber kein pi. Daher ist es nicht so, dass man mit pi eben genau dieses ausrechnen würde.

Aber klar: Damit gewinnt man auf Dauer keinen Blumentopf, da der Aufwand der Berechnung zu groß wird. Daher ist es ja auch so toll, dass es sowas wie die Kettenbrüche dafür gibt.... Aber das hilft dem TE nicht wirklich weiter.

 

[Meniskusschaden]

Wieso braucht ihr den Sinius nicht?

Wenn man ein Viertel des Einheitskreises mit gleich breiten Rechtecken füllt, kennt man ja die x-Positionen, an denen man mithilfe des Radius nach Pythagoras die Rechteckhöhen berechnen kann.

 

[White_Fox]

Entweder über Rechtecke integrieren, alternativ gibt es noch irgendein Taylorpolynom dafür was aber auf das Gleiche hinausläuft.

 

[Xyz1]

wieso ich da eine Skizze einfordere.

Ich auch, denn so raff ichs einfach nicht.

@White_Fox Man hat sich glaube ich viele Verfahren überlegt, um das mit dem Sinus zu vermeiden, also die Rechenarbeit zu minimieren - und die Genauigkeit zu erhöhen. Schließlich mussten das ein paar Schüler... eh... Sklaven per Hand ausrechnen.

 

[AndiE]

Ich bin da ja für den Desktest:

Ich nehme einen Kreis von r=100 .

Mit der Schrittweite s=10, wird

A1=h*s=100*10=1000

Nun berechne ich h neu mit
h=squrt(r*r-s*s)=sqrt(10000-100)=99,5

A2=h*s=99,5*10=995

h wird nun zu:

h=sqrt(r^2-(2s)^2)=sqrt(10000-400)=98

A3=h*s=980

so weiter bis h=sqrt(100^2-10*s^2=0 ist.

Insgesamt sollte ich dann als Summe alle An mit (n=1, bis 10) 31415... erhalten.

 

[mihe7]

Ich auch, denn so raff ichs einfach nicht.

Nimm die Skizze von @JustNobody - die grüne Linie ist die Hypotenuse im rechtwinkligen Dreieck, das mit roten, durchgezogenen Linien eingezeichnet ist, und entspricht dem Radius.

Die Länge des Streckenabschnitts auf der x-Achse ist bekannt (kumulierte Breite der Streifen). Die Länge des Hypotenuse ist bekannt. Folglich ist die Höhe des Dreiecks über den Pythagoras berechenbar.

Da die Höhe des Dreiecks der Höhe des Streifens entspricht und die Breite des Streifens (r/n) bekannt ist, kann die Fläche des Streifens berechnet werden. Aufsummieren, fertig.

 

[Xyz1]

Ist das nicht berühmt-berüchtigte Quadratur des Kreises?

 

[mihe7]

Damit Du Ruhe gibst:

 

[Meniskusschaden]

Müsste die Hypothenuse c nicht jeweils zur linken oberen Ecke des Rechteckes führen? Sonst entspricht ihre Länge doch nicht dem Radius.

 

[Xyz1]

Damit Du Ruhe gibst

Wird schon richtig sein. Ich like das mal und gebe ruhe.

 

[AndiE]

Wenn man das als Trapeze rechnet, würden diese Stützstellen rauskommen:
0-1
0,3-0,95
0,6-0,8
0,8 -0,6
0,95-0,3
1-0

Daraus wird

0,3*0,975+0,3*0,875+0,2*0,7+0,15*0,45+0,05*0,45=

0,2925+0,2625+0,14+0,0675+0,00075=0,76325

Erwartet werden Pi/4=0,78539

 

[Xyz1]

Trapeze

Nun wird's aber abenteuerlich...

 

[Vladyslav]

Habs! Vielen Dank für die starke Hilfe @all !

 

[mihe7]

Müsste die Hypothenuse c nicht jeweils zur linken oberen Ecke des Rechteckes führen? Sonst entspricht ihre Länge doch nicht dem Radius.

Das ist natürlich vollkommen richtig. Danke für die Klarstellung.

 

[Xyz1]

Ist denn nicht das damit gemeint

Der Flächeninhalt des Kreises - Zerlegung in Kreissektoren

Der Flächeninhalt des Kreises - Zerlegung in Kreissektoren

www.geogebra.org

Das Problem: Ich sehe die Zeichnung und könnte das auch ausschneiden und so hinlegen, aber die Formel erschließt sich mir nicht.

 

[White_Fox]

Dann schau dir mal die Formel für die Berechnung der Kreisfläche an...wenn du A(Rechteck) = x * r² umstellst:
x = A(Rechteck) / r²
wirst du feststellen, daß sich x an π annähert.

Edit:
Gibt es ein Latex-Plugin für das Forum? Das wäre mal nützlich.

 

[mihe7]

Gibt es ein Latex-Plugin für das Forum? Das wäre mal nützlich.

Ich mache das über einen Latex-Online Editor, der eine URL ausspuckt, die ich hier als Bild einfüge.

 

[mihe7]

Das Problem: Ich sehe die Zeichnung und könnte das auch ausschneiden und so hinlegen, aber die Formel erschließt sich mir nicht.

Das Problem ist, dass sich damit m. E. nur die Formel für die Kreisfläche herleiten lässt. Sind Umfang und Radius (und damit PI) bekannt, kann der Umfang in n gleichlange Teile geteilt und gezeigt werden, dass man sich durch Summe der Flächen der n gleichschenkligen Dreiecke mit Schenkellänge r an die Kreisfläche annähert.

 

[AndiE]

Nehmen wir mal an, ich schreibe ein Quadrat in einem Kreis. Dann ist bei einem r=10, die Seitenlänge 1/squrt(2)=14, da 14=sqrt(10^2+10^2) ist. 14*14=196, vom zu erwartenden Ergebnis von 314 also noch etwas weit entfernt. Das ist aber nicht wirklich der Weg: Die Fläche A besteht aus 4 Dreiecken, die jeweils eine Hypothenuse von 14 und eine Höhe von 7 haben, und somit wird A=4*A=4*14/7=49=196.

Die Frage ist doch, wie sich das verändert, wenn ich statt 4 nun 8 Tortenstückchen annehme. Wird die anzunehmende Verschachtelung von Wurzeln und Quadraten die Berechnung vereinfachen? Kann man das überhaupt als Normalsterblicher herleiten?

 

[Xyz1]

Blöde Frage, aber Pi ist doch die Kreisfläche des Einheitskreises - oder?

 

[White_Fox]

Nimm doch einfach mal den Höhensatz für rechtwinklinge Dreiecke. Die Höhe h ist gleich dem Radius r, wobei p und q gleich sind. Läßt sich daraus nix bauen?

Ich mache das über einen Latex-Online Editor, der eine URL ausspuckt, die ich hier als Bild einfüge.

Die Lösung kenne ich , finde ich persönlich aber wenig ansprechend.

 

[Xyz1]

So - ich habe mich eingelesen. Jetzt bin ich schon halb auf der Höhe. Die Kreisflächen-Integration scheint mir eine geeignete Wahl zu sein, um Pi näherungsweise zu ermitteln.
Nur - woher weiß man, auf wie viele Nachkommastellen genau das Ergebnis ist?

 

[White_Fox]

Nur - woher weiß man, auf wie viele Nachkommastellen genau das Ergebnis ist?

Integriere halt mit immer feineren Intervallen und schaue, auf welcher Nachkommastelle die Ergebnisse noch gleich bleiben.

 

[Xyz1]

Integriere halt mit immer feineren Intervallen und schaue, auf welcher Nachkommastelle die Ergebnisse noch gleich bleiben.

Das Problem ist, dass für das nächste Intervall die ersten Nachkommastellen gleich bleiben können, für über- oder überübernächste Intervalle aber nicht.
Insgesamt konvergiert das leider sehr langsam.
Hier etwas für alle, die ihre CPU quälen wollen

Spoiler

		long stop = Math.round(Math.PI * 10e5);
		for (int streifen = 2; streifen <= Integer.MAX_VALUE - 1; streifen++) {
			double sum = 0;
			for (int i = 0; i <= streifen; i++) {
				double x = 2.0 / streifen * i - 1.0;
				sum += Math.sqrt(1.0 - x * x) ;
			}
			sum = sum / streifen * 4;
			if (streifen % 1000 == 0) {
				System.out.println(streifen + " " + sum);
			}
			if (stop == Math.round(sum * 10e5)) {
				System.out.println(streifen + " " + sum);
				break;
			}
		}
		System.out.println(Math.PI);

 

[White_Fox]

streifen <= Integer.MAX_VALUE - 1

Ja, ich kann mir vorstellen daß das lange dauert.

Wie groß ist denn der Abstand, wenn du stattdessen nur mit 10.000 Streifen rechnest?

Edit: Füge doch noch eine Ausgabe von den Zeitpunkten von Start, Ende und Dauer der Berechnung ein.

 

[Xyz1]

Danke für die Müh.
Also die Kreisflächen-Integration scheint mir jetzt doch unpassend. ( Zumindest wenn man damit in einen Wettbewerb einsteigen möchte. )

 

[White_Fox]

Das kommt darauf an, was der Wettbewerb erreichen soll.

Ich hatte mal ein CPU-Benchmarkprogramm, dessen Bewertung auf der Zeit beruhte, die die CPU braucht um π auf 1.000.000 Stellen genau zu berechnen.

 

[Xyz1]

Ist doch Scheiße! Pi ist eine unnatürliche Zahl. Nichts auf der Welt ist zu 100% exakt rund oder eckig... Auch planetare Bahnen nicht. Man sollte sich gar nicht mit Pi beschäftigen.

 

[White_Fox]

Du solltest Geisteswissenschaftler werden.

 

[kneitzel]

Ist doch Scheiße! Pi ist eine unnatürliche Zahl. Nichts auf der Welt ist zu 100% exakt rund oder eckig... Auch planetare Bahnen nicht. Man sollte sich gar nicht mit Pi beschäftigen.

Ich denke, Archimedes hätte Dir widersprochen. Und er hat pi ohne Computer für damalige Verhältnisse sehr gut berechnet.