Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
Rekursion
- Themenstarter programmer77
- Beginndatum
Kannst du vl die Lösung bzw. den Lösungsweg schreiben ?
Wenn ich die Aufgabe lösen könnte, würde ich dann hier nicht posten. Das Problem ist, ich kann replicate() methode in diagonal nicht umsetzen...
BadBat
Aktives Mitglied
Kannst du vl die Lösung bzw. den Lösungsweg schreiben ?
Wenn ich jetzt die einfach die Lösung hinschreibe kannst DU es immernoch nicht...Wenn ich die Aufgabe lösen könnte, würde ich dann hier nicht posten. Das Problem ist, ich kann replicate() methode in diagonal nicht umsetzen...
Ok, danke ...
Robat
Top Contributor
Bei deiner Rekursionsaufgabe gibts erstmal 2 wesentliche Dinge die du beachten musst:
- Die Abbruchbedingung
- Sonst
Die Abbruchbedingung hast du ja schon jetzt musst du dir noch überlegen was du sonst machen willst.
Bei jedem neuen Rekursionsaufruf soll dein n um 1 verringert ausgegeben werden. (1. Punkt). [das sollte eigentlich machbar sein]
Jetzt muss vor jeder Zahl noch die richtige Anzahl an "_" stehen. Das machst du am besten mit einer for-Schleife. Die "Formel" [also die Abbruchbedingung der for-Schleife] um die richtige Anzahl auszugeben kannst du dir ja mal selber überlegen
- Die Abbruchbedingung
- Sonst
Die Abbruchbedingung hast du ja schon jetzt musst du dir noch überlegen was du sonst machen willst.
Bei jedem neuen Rekursionsaufruf soll dein n um 1 verringert ausgegeben werden. (1. Punkt). [das sollte eigentlich machbar sein]
Jetzt muss vor jeder Zahl noch die richtige Anzahl an "_" stehen. Das machst du am besten mit einer for-Schleife. Die "Formel" [also die Abbruchbedingung der for-Schleife] um die richtige Anzahl auszugeben kannst du dir ja mal selber überlegen
Man darf die Schleifen nicht verwenden, nur die Rekursion.Bei deiner Rekursionsaufgabe gibts erstmal 2 wesentliche Dinge die du beachten musst:
- Die Abbruchbedingung
- Sonst
Die Abbruchbedingung hast du ja schon jetzt musst du dir noch überlegen was du sonst machen willst.
Bei jedem neuen Rekursionsaufruf soll dein n um 1 verringert ausgegeben werden. (1. Punkt). [das sollte eigentlich machbar sein]
Jetzt muss vor jeder Zahl noch die richtige Anzahl an "_" stehen. Das machst du am besten mit einer for-Schleife. Die "Formel" um die richtige Anzahl auszugeben kannst du dir ja mal selber überlegen
Und die Zahlen um 1 verringern ist schon klar.
System.out.println(n);
diagonal(m,n-1);
Aber wie man die replicate meth hier einsetzen soll, kA .
System.out.println(n);
diagonal(m,n-1);
Aber wie man die replicate meth hier einsetzen soll, kA .
Mit replicate ('_', n-m) kann man aber die replicate meth aufrufen .
BadBat
Aktives Mitglied
Die willste ja in diagonal garnicht aufrufen.Mit replicate ('_', n-m) kann man aber die replicate meth aufrufen .
m und _ hängen auch zusammen sowie m auch wichtig für deine terminierung ist
Danke für deine Bemühung, gehts leider nicht.Die willste ja in diagonal garnicht aufrufen.
m und _ hängen auch zusammen sowie m auch wichtig für deine terminierung ist
Robat
Top Contributor
Und die Zahlen um 1 verringern ist schon klar.
System.out.println(n);
diagonal(m,n-1);
Dann stell deine Frage nächstes mal genauer .. dann kann man sich das rumgerate sparen
Ich würde übrigens noch mal die replicate(char, int) Methode anschauen. Die wird nicht das machen was du erwartest
Du musst in deiner diag(int, int) Methode erst die replicate Methode aufrufen und danach die Zahl ausgeben. Denk immer daran dass es auf der selben Zeile sein soll daher nicht println sonder nur print verwenden. Die Anzahl der Zeichen kannst du nicht über
n - m bestimmen. Du musst diese Differenz noch in Zusammenhang mit der Anzahl der Zeichen bringen.
Zuletzt bearbeitet:
Replicate methode
replicate -> gibt das Zeichen c n-mal aus.Dann stell deine Frage nächstes mal genauer .. dann kann man sich das rumgerate sparen
Ich würde übrigens noch mal die replicate Methode anschauen. Die wird nicht das machen was du erwartest
Robat
Top Contributor
Aber nicht in der Form wie du es bei derreplicate -> gibt das Zeichen c n-mal aus.
diag(int,int) Methode brauchst BadBat
Aktives Mitglied
Da der ersteller jetzt eh offline ist und damit das nicht nen mülltonnen eintrag wird den niemand was nützt hier nochmal die Lösung.
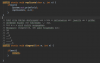
Java:
/**
* Hier System.out.print(); verwenden nicht System.out.println(LINE)();
* Da sonst jeder underscore in eine eigene Zeile geschrieben wird.
*/
public static void replicate(char c, int n) {
if (n > 0) {
System.out.print(c);
replicate(c, n - 1);
}
}
/**
* Wenn m = 5 und n = 10 ist n-m die anzahl der benötigten underscores.
* Dann wird Rekursiv aufgerufen und m um einen erhöht.
* Terminierung der Rekursion ist erreicht sobald m = n ist
* dann muss nurnoch n ausgegeben werden.
*/
public static void diagonal(int m, int n){
if(m<n){
diagonal(m + 1, n);
replicate('_', n-m);
System.out.println(m);
}
else{
System.out.println(n);
}
}
public static void main(String[] args) {
diagonal(5,10);
}Ähnliche Java Themen
Ähnliche Java Themen
-
-
-
-
Variablen Rekursion mit 2 Parameteren
- Gestartet von munto
- Antworten: 4
-
Rekursion größten Primfaktor finden funktioniert nicht
- Gestartet von sserio
- Antworten: 8
-
-
-
-
-
Vokale in einem String überprüfen mittels Rekursion
- Gestartet von P9cman
- Antworten: 8
-
-
-
Rekursion: Rechenmauer mit Array erstellen
- Gestartet von Krön
- Antworten: 17
-
Rekursion einer Zahlenfolge (Ab- und Aufzählung)
- Gestartet von Krön
- Antworten: 6
-
-
-
-
-
for Schleife durch Rekursion ersetzen
- Gestartet von nikva
- Antworten: 6
-
-
-
-
Rekursion Tage Ansteckung gesamte Bevölkerung
- Gestartet von Martina1909
- Antworten: 15
-
-
-
-
-
Verständnisproblem der Rekursion bei Arrays
- Gestartet von Mika34
- Antworten: 8
-
-
Klassen Rekursion mit Feldern von Objekten
- Gestartet von nightrider
- Antworten: 14
-
-
Konsolenausgabe Zahlenfolge Rekursion
- Gestartet von DevZ02
- Antworten: 3
-
-
-
B
-
-
-
-
-
Mit Rekursion Zufallszahlen erstellen und größte finden
- Gestartet von aidaleon
- Antworten: 5
-
-
-
-
-
-
-
-
-
-
Bitte um Hilfe bei Quellcode (Rekursion)
- Gestartet von mb77-97
- Antworten: 6
-
Rekursion Warum bricht meine Funktion nicht ab
- Gestartet von trytocatch
- Antworten: 4
-
Hilfe bei Rekursion,Ich verstehe nicht,wie funktioniert die Rekursion in der Methode "walk"
- Gestartet von Alaa
- Antworten: 13
-
-
Pfade eines Baums angeben ohne Rekursion
- Gestartet von ernst
- Antworten: 20
-
-
-
-
-
-
Methoden zur Rekursion (catalansche Zahlen)
- Gestartet von NicoBec
- Antworten: 4
-
-
Java catalansche Zahlen (Rekursion)
- Gestartet von NicoBec
- Antworten: 5
-
-
-
Methoden Abbruchbedingung bei Rekursion
- Gestartet von FridolinF
- Antworten: 2
-
-
-
Methoden Rekursion gibt alten Wert wieder
- Gestartet von lollipol27
- Antworten: 37
-
-
-
Aufgabe Rekursion Binärer Baum
- Gestartet von FuckinDonuts
- Antworten: 15
-
-
-
Problem beim grundsätzlichen Verständnis bei Rekursion mit 2-dimensionalen Array
- Gestartet von Blacktycho
- Antworten: 6
-
-
-
Rekursion Funktion in eine Iterativ Funktion umwandeln
- Gestartet von AClassyWarius
- Antworten: 9
-
-
-
-
-
Rekursion stoppt an der falschen Stelle
- Gestartet von asyoulikeit
- Antworten: 4
-
-
-
Rekursion Schneeflocke - Kurze Frage zur Methode
- Gestartet von bob651
- Antworten: 11
-
-
Rekursion Rückgabe - Türme von Hanoi
- Gestartet von SnowDragon
- Antworten: 16
-
-
-
Grekursion nicht verstanden
- Gestartet von Gelöschtes Mitglied 54019
- Antworten: 5
-
-
Methoden String wird in Rekursion nicht überschrieben
- Gestartet von Escape99X
- Antworten: 2
-
-
-
Methoden Zahlensysteme umwandeln mittels Rekursion
- Gestartet von Kahoona510
- Antworten: 5
-
-
Methoden Primzahltest mit Rekursion
- Gestartet von pinkcrime
- Antworten: 3
-
Rekursion überführen in eine normale methode
- Gestartet von canyakan95
- Antworten: 1
-
-
Aktuelle Jobs
-
Wafios Softwareentwickler Cloud (JAVA/Spring) m/w/d - Reutlingen
- Gestartet von Java_Jobs
- Antworten: 0
-
Inek Senior Java Softwareentwickler (m/w/d) - Siegburg
- Gestartet von Java_Jobs
- Antworten: 0
-
Atos Senior Java Architekt (m/w/d) - Fürth
- Gestartet von Java_Jobs
- Antworten: 0
-
-
FCA Bank Java-Entwickler (m/w/d) (Heilbronn)
- Gestartet von Java_Jobs
- Antworten: 0
Neue Themen
-
-
-
Swing Swing - Eigene Komponenten erstellen
- Gestartet von White_Fox
- Antworten: 7
-
Auslesen Datums-Daten von Web-Graphic mit JavaScript
- Gestartet von J90
- Antworten: 4
-