Ich hab von einer Freundin folgende Aufgabe erhalten:
Sissa ibn Dahir lebte angeblich im dritten oder vierten Jahrhundert n. Chr. in Indien und gilt Legenden zufolge als der Erfinder des Schachspiels beziehungsweise seiner indischen Urform Caturanga. Sein Name ist mit der Reiskornlegende (auch als Schachbrettaufgabe bekannt) verbunden. Die Geschichte ist ein „Gleichnis für die Vielfalt des Schachspiels“, welches die Unerschöpflichkeit der Möglichkeiten und Partieverläufe im Schach versinnbildlicht. Der indische Herrscher Shihram tyrannisierte seine Untertanen und stürzte sein Land in Not und Elend. Um die Aufmerksamkeit des Königs auf seine Fehler zu lenken, ohne seinen Zorn zu entfachen, schuf Dahirs Sohn, der weise Bramahne Sissa, ein Spiel, in dem der König als wichtigste Figur ohne Hilfe anderer Figuren und Bauern nichts ausrichten kann. Der Unterricht im Schachspiel machte auf Shihram einen starken Eindruck. Er wurde milder und liess das Schachspiel verbreiten, damit alle davon Kenntnis nähmen. Um sich für die anschauliche Lehre von Lebensweisheit und zugleich Unterhaltung zu bedanken, gewährte er dem Brahmanen einen freien Wunsch. Dieser wünschte sich Reiskörner: Auf das erste Feld eines Schachbretts wollte er ein Korn, auf das zweite Feld das Doppelte, also zwei, auf das dritte wiederum die doppelte Menge, also vier, und so weiter. Der König lachte und war gleichzeitig erbost über die vermeintliche Bescheidenheit des Brahmanen. Als sich Shihram einige Tage später erkundigte, ob Sissa seine Belohnung in Empfang genommen habe, musste er hören, dass die Rechenmeister die Menge der Reiskörner noch nicht berechnet hätten. Der Vorsteher der Kornkammer meldete nach mehreren Tagen ununterbrochener Arbeit, dass er diese Menge Reiskörner im ganzen Reich nicht aufbringen könne. Nun stellte er sich die Frage, wie das Versprechen eingelöst werden könne. Der Rechenmeister half dem Herrscher aus der Verlegenheit, indem er ihm empfahl, er solle Sissa ibn Dahir ganz einfach das Reis Korn für Korn zählen lassen.
Gib für jede Schachfeldnummer die zugehörige Reiskornzahl aus.
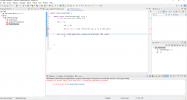
Nun habe ich 2 For-Schleifen ineinander verschachtelt (macht das überhaupt Sinn?), aber z.B. die Math.pow(x,y)-Funktion funktioniert überhaupt nicht und bei der Variablen-Setzung habe ich auch etwas falsch gemacht.
public class WeiserInder {
public static void main(String[] args) {
// TODO Auto-generated method stub
int i = 1;
int j = 0;
for (i = 1; i <= 64; i++);}{ for (j = i -1; j <=63; j++);
int result = Math.pow(2,j);}; System.out.println(i; " "; result
)}
}
}
Sissa ibn Dahir lebte angeblich im dritten oder vierten Jahrhundert n. Chr. in Indien und gilt Legenden zufolge als der Erfinder des Schachspiels beziehungsweise seiner indischen Urform Caturanga. Sein Name ist mit der Reiskornlegende (auch als Schachbrettaufgabe bekannt) verbunden. Die Geschichte ist ein „Gleichnis für die Vielfalt des Schachspiels“, welches die Unerschöpflichkeit der Möglichkeiten und Partieverläufe im Schach versinnbildlicht. Der indische Herrscher Shihram tyrannisierte seine Untertanen und stürzte sein Land in Not und Elend. Um die Aufmerksamkeit des Königs auf seine Fehler zu lenken, ohne seinen Zorn zu entfachen, schuf Dahirs Sohn, der weise Bramahne Sissa, ein Spiel, in dem der König als wichtigste Figur ohne Hilfe anderer Figuren und Bauern nichts ausrichten kann. Der Unterricht im Schachspiel machte auf Shihram einen starken Eindruck. Er wurde milder und liess das Schachspiel verbreiten, damit alle davon Kenntnis nähmen. Um sich für die anschauliche Lehre von Lebensweisheit und zugleich Unterhaltung zu bedanken, gewährte er dem Brahmanen einen freien Wunsch. Dieser wünschte sich Reiskörner: Auf das erste Feld eines Schachbretts wollte er ein Korn, auf das zweite Feld das Doppelte, also zwei, auf das dritte wiederum die doppelte Menge, also vier, und so weiter. Der König lachte und war gleichzeitig erbost über die vermeintliche Bescheidenheit des Brahmanen. Als sich Shihram einige Tage später erkundigte, ob Sissa seine Belohnung in Empfang genommen habe, musste er hören, dass die Rechenmeister die Menge der Reiskörner noch nicht berechnet hätten. Der Vorsteher der Kornkammer meldete nach mehreren Tagen ununterbrochener Arbeit, dass er diese Menge Reiskörner im ganzen Reich nicht aufbringen könne. Nun stellte er sich die Frage, wie das Versprechen eingelöst werden könne. Der Rechenmeister half dem Herrscher aus der Verlegenheit, indem er ihm empfahl, er solle Sissa ibn Dahir ganz einfach das Reis Korn für Korn zählen lassen.
Gib für jede Schachfeldnummer die zugehörige Reiskornzahl aus.
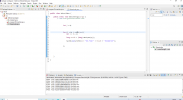
Nun habe ich 2 For-Schleifen ineinander verschachtelt (macht das überhaupt Sinn?), aber z.B. die Math.pow(x,y)-Funktion funktioniert überhaupt nicht und bei der Variablen-Setzung habe ich auch etwas falsch gemacht.
public class WeiserInder {
public static void main(String[] args) {
// TODO Auto-generated method stub
int i = 1;
int j = 0;
for (i = 1; i <= 64; i++);}{ for (j = i -1; j <=63; j++);
int result = Math.pow(2,j);}; System.out.println(i; " "; result
)}
}
}