Hallo, bin die ganze Zeit am Rumdenken komme aber auf nichts Vernünftiges.
Aufgabe:
Zwei Listen Folgen den Regeln der Mengenlehre (es dürfen keine doppelten Elemente in einer Liste sein) ich soll nun die Methode Vereinigung (
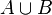 ) schreien, die steht auch und funktioniert. Jetzt soll sie optimiert werden und in O(m+n) durchlaufen, dabei steht n für die Hauptliste und m für die neue Liste, die dazukommt.
) schreien, die steht auch und funktioniert. Jetzt soll sie optimiert werden und in O(m+n) durchlaufen, dabei steht n für die Hauptliste und m für die neue Liste, die dazukommt.
Also durchläuft die Methode einmal Liste 1 und einmal Liste 2 (?)
Momentane Situation:
Ich durchlaufe in der Methode die zweite Liste mit einem Iterator und Vergleiche jedes Element mit der in der ersten Liste mithilfe der Methodecontains, die auch nur eine Art Iterator ist. Also bin ich bei... m + n^n (n hoch n) ?
Egal wie ich es drehe und wende ich komme nicht darauf, wie ich es optimieren kann. Es wird ja am ende immer ein Vergleich benötigt, wenn ein neues Element dazu kommt(da es keine doppelten werte haben darf [ich teste es gerade mit Integer]).
Aufgabe:
Zwei Listen Folgen den Regeln der Mengenlehre (es dürfen keine doppelten Elemente in einer Liste sein) ich soll nun die Methode Vereinigung (
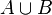
Also durchläuft die Methode einmal Liste 1 und einmal Liste 2 (?)
Momentane Situation:
Ich durchlaufe in der Methode die zweite Liste mit einem Iterator und Vergleiche jedes Element mit der in der ersten Liste mithilfe der Methodecontains, die auch nur eine Art Iterator ist. Also bin ich bei... m + n^n (n hoch n) ?
Egal wie ich es drehe und wende ich komme nicht darauf, wie ich es optimieren kann. Es wird ja am ende immer ein Vergleich benötigt, wenn ein neues Element dazu kommt(da es keine doppelten werte haben darf [ich teste es gerade mit Integer]).
