Perfektes Mischen

[BlueLizard]

Ich weiß, noch ein Thema und dann um die Uhrzeit aber ich brauche noch ein Denkanstoß, diese Woche ist echt der Wurm drin.

Ich soll folgende Aufgabe bearbeiten:

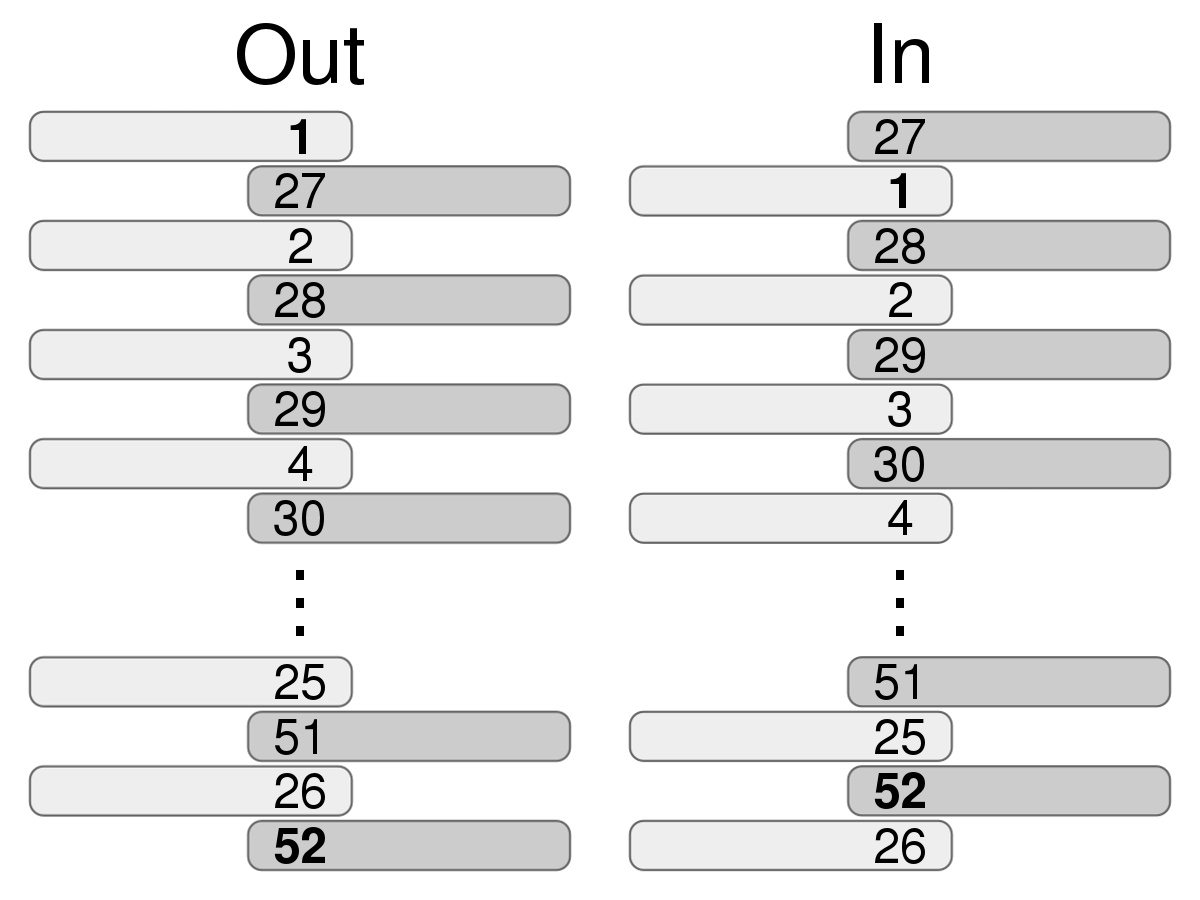
Wird ein Kartenspiel oft genug perfekt gemischt, nimmt er seine ursprüngliche Reihenfolge wieder an.
Schreiben Sie nun eine Methode die eine beliebige gerade Zahl n>0 als Größe eines Kartenstapels akzeptiert. Die Methode gibt zurück, wie oft ein Kartenstapel dieser Größe höchstens perfekt gemischt werden muss, damit er seine ursprüngliche Reihenfolge wieder annimmt.

Beispiel ist ein Kartenspiel n=52 als Ergebnis soll 8 raus kommen.

Ich habe noch 2 andere Methoden zur Verfügung (welche bereits auf richtigkeit überprüft wurden ):

  public static int[] interleave(int[] a1, int[] a2) {
    int[] a3 = new int[a1.length + a2.length];
    for (int i = 0; i < a1.length;) {
      for (int j = 0; j < a3.length; ) {
        a3[j] = a1[i];
        j = j + 2;
        i++;
      }
    }

    for (int i = 0; i < a2.length;) {
      for (int j = 1; j < a3.length; ) {
        a3[j] = a2[i];
        j = j + 2;
        i++;
      }
    }
    return a3;
  }

  public static int[] perfectShuffle(int[] a) {
    if (a.length % 2 != 0) return a;
    int j=0;
    int zähl=0;
    int[] b = new int[a.length/2];
    int[] c = new int[a.length/2];
    for (int i = 0;i < b.length;i++) {
      b[i] = a[i];
      j++;
    }
    for (int i = 0;i < c.length;i++) {
      c[i] = a[j];
      j++;
      }
    a = interleave(b,c);
    return a;
  }

Meine eigentliche Frage ist jetzt wie man sowas berechnen kann? Da muss es ja einen Zusammenhang geben. Mir würde vermutlich ein Wort schon reichen

Danke für die Hilfe im Vorraus schon mal

 

[thecain]

Faro shuffle - Wikipedia

en.m.wikipedia.org

 

[BlueLizard]

Faro shuffle - Wikipedia

en.m.wikipedia.org

Danke erstmal dafür.

Ich verstehe nur nicht so ganz. Das Beispiel in dem Artikel zeigt ja 2^8 soll identisch mit 1 (mod 51) sein. Wie berecht man sowas in Java?

 

[mihe7]

Naja 2^k = 1 mod (n-1) bedeutet ja, dass (2^k) mod (n-1) = 1 mod (n-1) = 1. In Java muss also gelten Math.pow(2,k) % (n-1) == 1. Oder umgekehrt: es muss eine ganze Zahl z geben mit z*(n-1)+1=Math.pow(2,k). Im konkreten Fall wäre n=52, z = 5 und k = 8.

 

[BlueLizard]

Naja 2^k = 1 mod (n-1) bedeutet ja, dass (2^k) mod (n-1) = 1 mod (n-1) = 1. In Java muss also gelten Math.pow(2,k) % (n-1) == 1. Oder umgekehrt: es muss eine ganze Zahl z geben mit z*(n-1)+1=Math.pow(2,k). Im konkreten Fall wäre n=52, z = 5 und k = 8.

Ja auf z =5 komme ich auch, aber auf k=8 komme ich einfach nicht.

Mein Code:

  public static int shuffleNumber(int n) {
    //Idee: 2^ shuffelnumer kongruent 1  (mod n-1)
    int z = (int) (Math.log(n) /Math.log(2));
    if (n % 2 != 0) return -1;
    else {
     return (int) (Math.log(z*(n-1)+1) / Math.log(2));
    }

  }

 

[mihe7]

Ja auf z =5 komme ich auch, aber auf k=8 komme ich einfach nicht.

Wie meinst Du das? Wenn Du z = 5 hast, dann ist z*(n-1)+1 = 256 und der 2er-Logarithmus von 256 ist 8.

 

[BlueLizard]

Wie meinst Du das? Wenn Du z = 5 hast, dann ist z*(n-1)+1 = 256 und der 2er-Logarithmus von 256 ist 8.

Guck meinen Code an. Für 52 kommt jetzt 8 raus, aber der automatische Test sagt immernoch das es nicht stimmt..


Fehler:
There was 1 failure: 1) testPerfectShuffle(PerfectShuffleTest) java.lang.AssertionError: shuffleNumber computes wrong result. expected:<6> but was:<4> at PerfectShuffleTest.testPerfectShuffle(PerfectShuffleTest.java:86)

 

[insanezulu]

Na, hier ist doch nicht wirklich ein Problem...

public static int log2(int x) {
	return (int) (Math.log(x) / Math.log(2));
}

public static int pow2(int x) {
	return (int) Math.pow(2, x);
}

public static int a(int x) {
	return log2(log2(x) * (x - 1) + 1);
}

public static int b(int x) {
	return pow2(x) / (x + 1);
}

public static void main(String[] args) {
	int[] c = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 };

	for (int i = 0; i < c.length; i++) {
		int d = c[a(i)];
		c[a(i)] = c[i];
		c[i] = d;
	}
	System.out.println(Arrays.toString(c));

	for (int i = c.length - 1; i >= 0; i--) {
		int d = c[a(i)];
		c[a(i)] = c[i];
		c[i] = d;
	}
	System.out.println(Arrays.toString(c));
}

Es gibt zu "a" nur nicht wirklich eine Umkehrfunktion.

 

[mihe7]

public int maxShuffle(int even) {
    if ((even & 1) != 0) { throw new IllegalArgumentException(even + " ist keine gerade Zahl."); }
    int r = 1;
    int k = 0;
    do {
        k++;
        r <<= 1;
    } while (r % (even-1) != 1);
    return k;
}

 

[insanezulu]

Das ist ja komplett anders als meins... Ich glaub wir reden alle aneinander vorbei....

 

[BlueLizard]

public int maxShuffle(int even) {
    if ((even & 1) != 0) { throw new IllegalArgumentException(even + " ist keine gerade Zahl."); }
    int r = 1;
    int k = 0;
    do {
        k++;
        r <<= 1;
    } while (r % (even-1) != 1);
    return k;
}

Danke erstmal für deine Antwort.

Allerdings mehrere Fragen:

Was macht:
1. das even & 1?
2. r <<= 1;
Also mir ist klar das es bitweise operatoren sind, aber genauer habe ich mich noch nicht damit beschäftigt.

Diese Version determiniert übrigens für bestimmte werte nicht (etwa 98, 2, 68,38).

 

[mihe7]

Das ist ja komplett anders als meins... Ich glaub wir reden alle aneinander vorbei....

Seine Frage war: wie berechne ich das k, wenn 2^k mod (n-1) = 1 mod (n-1) gelten soll. Die Methode sollte das k für ein gegebenes, gerades n berechnen, wenn ich mich nicht vertan habe.

Kürzer sollte es so gehen:

int k;
for (k = 1;  (1 << k) % (n-1) != 1; k++) 
    ;
return k;

 

[BlueLizard]

Seine Frage war: wie berechne ich das k, wenn 2^k mod (n-1) = 1 mod (n-1) gelten soll. Die Methode sollte das k für ein gegebenes, gerades n berechnen, wenn ich mich nicht vertan habe.

Kürzer sollte es so gehen:

int k;
for (k = 1;  (1 << k) % (n-1) != 1; k++)
    ;
return k;

Danke nochmal für deine Hilfe, damit geht jetzt alles !

 

[mihe7]

Was macht:
1. das even & 1?
2. r <<= 1;
Also mir ist klar das es bitweise operatoren sind, aber genauer habe ich mich noch nicht damit beschäftigt.

1. extrahiert das 1. Bit. Wenn dieses 1 ist, ist die Zahl ungerade, sonst gerade.
2. r <<=1 ist die Kurzform für r = r << 1. r wird um 1 Bit nach links geschiftet, das ist einfach eine Multiplikation mit 2. Sprich: r <<= 1 ist das gleiche wie r = r * 2 (oder r *= 2).

Im Klartext:

public int maxShuffle(int even) {
    if ((even % 2) != 0) { throw new IllegalArgumentException(even + " ist keine gerade Zahl."); }
    int r = 1;
    int k = 0;
    do {
        k++;
        r = r * 2;
    } while (r % (even-1) != 1);
    return k;
}

Diese Version determiniert übrigens für bestimmte werte nicht (etwa 98, 2, 68,38).

Richtig: für 2 terminiert sie nicht, weil r % 1 immer 0 ist. Bei k > 31 gibt es aktuell einen Overflow bei r (int hat ja nur 32 Bit). Um dem entgegen zu wirken, wäre in der Schleife % (even - 1) zu rechnen:

public int maxShuffle(int even) {
    if ((even % 2) != 0) { throw new IllegalArgumentException(even + " ist keine gerade Zahl."); }
    int r = 1;
    int k = 0;
    do {
        k++;
        r = (r * 2) % (even - 1);
    } while (r != 1);
    return k;
}

Nebenbei: der Code ist nur ein Teil der Lösung für Deine Aufgabe.

 

[BlueLizard]

1. extrahiert das 1. Bit. Wenn dieses 1 ist, ist die Zahl ungerade, sonst gerade.
2. r <<=1 ist die Kurzform für r = r << 1. r wird um 1 Bit nach links geschiftet, das ist einfach eine Multiplikation mit 2. Sprich: r <<= 1 ist das gleiche wie r = r * 2 (oder r *= 2).

Im Klartext:

public int maxShuffle(int even) {
    if ((even % 2) != 0) { throw new IllegalArgumentException(even + " ist keine gerade Zahl."); }
    int r = 1;
    int k = 0;
    do {
        k++;
        r = r * 2;
    } while (r % (even-1) != 1);
    return k;
}

Richtig: für 2 terminiert sie nicht, weil r % 1 immer 0 ist. Bei k > 31 gibt es aktuell einen Overflow bei r (int hat ja nur 32 Bit). Um dem entgegen zu wirken, wäre in der Schleife % (even - 1) zu rechnen:

public int maxShuffle(int even) {
    if ((even % 2) != 0) { throw new IllegalArgumentException(even + " ist keine gerade Zahl."); }
    int r = 1;
    int k = 0;
    do {
        k++;
        r = (r * 2) % (even - 1);
    } while (r != 1);
    return k;
}

Nebenbei: der Code ist nur ein Teil der Lösung für Deine Aufgabe.

Wurde soweit verstanden und ja ich weiß das es nur ein Teil der Lösung ist. Die Aufgabe an sich ist auch viel länger ich kam nur mit diesem Teilproblem nicht klar, weil ich zum einen nicht wusste welche Mathematische Zusammenhang dahinter steckt und zum anderen weil mir da einfach nur die Erfahrung beim Programmieren fehlt. Deshalb vielen Dank für deinen Input, das hat mich nicht nur bei der Aufgabe weiter gebracht sondern auch Programmiertechnisch.

 

[mihe7]

Ich bin ja immer noch auf der Suche nach einem mathematischen Trick, um das k einfacher zu berechnen. Zumindest wäre die untere Grenze von k bekannt: [(log(n)/log(2)], mit [x] = kleinste ganze Zahl größer gleich x. Das wäre bei n = 52 dann die 6.