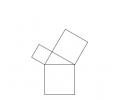
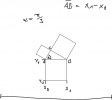
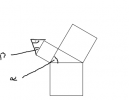
public class PythagorasTree {
public static double sitesX (double angle, double x) {
double p = Math.cos(angle) * x;
return Math.cos(angle) * p;
}
public static double sitesY (double angle, double y) {
double p = Math.cos(angle) * y;
return Math.sin(angle) * p;
}
public static void drawH (int N ,double x, double y, double size) {
if (N == 0) return;
double angle = Math.PI/3;
double x0 = x - size/5;
double x1 = x + size/5;
double y0 = y - size/5;
double y1 = y + size/5;
StdDraw.line(x0, y0, x0, y1);
StdDraw.line(x1, y0, x1, y1);
StdDraw.line(x0, y0, x1, y0);
StdDraw.line(x0, y1, x1, y1);
double gegenkatheteLaenge = Math.sin(angle) * (x1-x0);
double ankatheteLaenge = Math.cos(angle) * (x1-x0);
double rechtesQuadrat1 = gegenkatheteLaenge * Math.sin(angle);
double rechtesQuadrat2 = gegenkatheteLaenge * Math.cos(angle);
double linkesQuadrat1 = ankatheteLaenge * Math.sin(angle);
double linkesQuadrat2 = ankatheteLaenge * Math.cos(angle);
// Dreieck
StdDraw.line(x0, y1, x0 + sitesX(angle, x1-x0), y1 + sitesY(angle, x1-x0));
StdDraw.line(x1, y1, x0 + sitesX(angle, x1-x0), y1 + sitesY(angle, x1-x0));
// Rechtes Quadrat
StdDraw.line(x0 + sitesX(angle, x1-x0), y1 + sitesY(angle, x1-x0),
x0 + sitesX(angle, x1-x0) + rechtesQuadrat2,
y1 + sitesY(angle, x1-x0) + rechtesQuadrat1);
StdDraw.line(x1,y1, x1 + rechtesQuadrat2,
y1 + rechtesQuadrat1);
StdDraw.line(x1 + rechtesQuadrat2,y1 + rechtesQuadrat1, x0 +
sitesX(angle, x1-x0) + rechtesQuadrat2,
y1 + sitesY(angle, x1-x0) + rechtesQuadrat1);
// Linkes Quadrat
StdDraw.line(x0, y1, x0 - linkesQuadrat1, y1 + linkesQuadrat2);
StdDraw.line(x0 + sitesX(angle, x1-x0) , y1 + sitesY(angle, x1-x0),
x0 + sitesX(angle, x1-x0) - linkesQuadrat1, y1 + sitesY(angle, x1-x0) + linkesQuadrat2);
StdDraw.line(x0 + sitesX(angle, x1-x0) - linkesQuadrat1, y1 + sitesY(angle, x1-x0) + linkesQuadrat2
, x0 - linkesQuadrat1, y1 + linkesQuadrat2);
}
public static void main(String[] args) {
int N = 4;
double x0 = 0.5 - 0.5/5;
double x1 = 0.5 + 0.5/5;
double y0 = 0.1 - 0.5/5;
double y1 = 0.1 + 0.5/5;
drawH(N, 0.5, .1, .5);
}
}