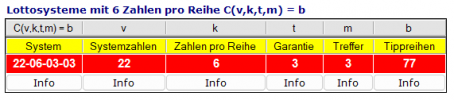
Wobei ich es an dem simplen beispiel mal kurz durchspielen will:
Zu Beginn spielen wir Lottt 3aus6 und wollen 3 Richtige. heißt auch dass wir 3 zahlen aus 1-6 ziehen (pro tippreihe) und 3 gewinnzhaleen gezogen werden.
Nun überlegen wir uns, wenn wir die zahlenmenge in 2 Bereiche aufteilen, wie es sich dann verhält.
Aus gewissen Gründen nehmen wir eine 3-3 Zerlegung (man hätte theoretisch auch 2 zahlen in A und 4 in B legen können. würde am Ende aber wohl zuv viele Tippreihen bedeuten, weshalb man es so wählt)
heißt also, die zahlen 1-3 liegen nun in A und die zahlen 4-6 in B.
Was heißt das nun im Weiteren zur verteilung der gewinnzahlen?
es gibt praktisch nur die aufteilungen 3-0 2-1 1-2 0-3
weil wir ja 2 richtige haben wollen, prüfen wir tippreihen die den fall abdekcen dass 2 gewinnzahlen in A sind.
und gewinnreihen für den fall dass 2 gewinnzahlen in B sind.
das heißt, wir spilen nun 2 separate lottospiele:
Lotto 3 aus 3, gesucht 2 richtige. (mit zahlenbereich 1-3)
und lotto 3aus3, gesucht 2 richtige (mit zahlenbereich 4-6)
ich schreibs extra 2 mal hin, obwohl identisch, da es im großen fall mit 6aus49 und 3 richtigen eben 2 ungleiche gruppengrößen gibt.
Naja, ohne zu überlegen ist klar:
wenns nur 3 zahlen gibt und wir 3 zahlen tippen dürfen, dann machen wir halt eine tippreihe mit genau den 3 zahlen.
daher lösen wir das erste lottospiel durhc eine tippreihe (1,2,3)
und das zweite lottospiel durch eine tippreihe (4,5,6).
Was mir so nebenher auffiel was man "falsch" machen kann:
Auch ich dachte anfangs bei den zerlegungen oben drüber nach, warum man bspw. nicht 2 lottospiele 3aus3, 1 zahl wird gezogen macht.
denn wenn man alle fälle mit 1 gewinnzahl in A und alle fälle mit 1 gewinnfall in B abdeckt, hat man doch auch alle konfigurationen, richtig?und es würde sogar weniger tippreihen brauchen, nciht wahr?
tja, leider falsch.
Denn wir wollen ja 2(!) richtige!
Und wenn in einer menge A nur 1 gewinnzahl vorkommt, können wir tippen was wir wollen und werden niemals 2 richtige haben!
Daher ist auch die untergrenze für die gewinnzahlen pro menge, wie wir es aufteilen sollten, immer gleich der gesuchten zahl an richtigen.
darum würde es auch keinen sinn machen, im sinne der informatik das 3aus3 , mit 2 hgewinnzahlen, irgendwie npchmal in 2 Mengen
P und Q zu zerlegen. dann hätte p 1 element und q 2 oder umgekehrt.
nie im leben könnte man mit elementen aus der jeweiligen gruppe 2 richtige hinkriegen, die einelementige gruppe könnte keine 2 richtige hervorbringen.
wie man das Alles mathematisch ermitteln kann?
keine Ahnung, das wüssten wir alle gern
Zu Beginn spielen wir Lottt 3aus6 und wollen 3 Richtige. heißt auch dass wir 3 zahlen aus 1-6 ziehen (pro tippreihe) und 3 gewinnzhaleen gezogen werden.
Nun überlegen wir uns, wenn wir die zahlenmenge in 2 Bereiche aufteilen, wie es sich dann verhält.
Aus gewissen Gründen nehmen wir eine 3-3 Zerlegung (man hätte theoretisch auch 2 zahlen in A und 4 in B legen können. würde am Ende aber wohl zuv viele Tippreihen bedeuten, weshalb man es so wählt)
heißt also, die zahlen 1-3 liegen nun in A und die zahlen 4-6 in B.
Was heißt das nun im Weiteren zur verteilung der gewinnzahlen?
es gibt praktisch nur die aufteilungen 3-0 2-1 1-2 0-3
weil wir ja 2 richtige haben wollen, prüfen wir tippreihen die den fall abdekcen dass 2 gewinnzahlen in A sind.
und gewinnreihen für den fall dass 2 gewinnzahlen in B sind.
das heißt, wir spilen nun 2 separate lottospiele:
Lotto 3 aus 3, gesucht 2 richtige. (mit zahlenbereich 1-3)
und lotto 3aus3, gesucht 2 richtige (mit zahlenbereich 4-6)
ich schreibs extra 2 mal hin, obwohl identisch, da es im großen fall mit 6aus49 und 3 richtigen eben 2 ungleiche gruppengrößen gibt.
Naja, ohne zu überlegen ist klar:
wenns nur 3 zahlen gibt und wir 3 zahlen tippen dürfen, dann machen wir halt eine tippreihe mit genau den 3 zahlen.
daher lösen wir das erste lottospiel durhc eine tippreihe (1,2,3)
und das zweite lottospiel durch eine tippreihe (4,5,6).
Was mir so nebenher auffiel was man "falsch" machen kann:
Auch ich dachte anfangs bei den zerlegungen oben drüber nach, warum man bspw. nicht 2 lottospiele 3aus3, 1 zahl wird gezogen macht.
denn wenn man alle fälle mit 1 gewinnzahl in A und alle fälle mit 1 gewinnfall in B abdeckt, hat man doch auch alle konfigurationen, richtig?und es würde sogar weniger tippreihen brauchen, nciht wahr?
tja, leider falsch.
Denn wir wollen ja 2(!) richtige!
Und wenn in einer menge A nur 1 gewinnzahl vorkommt, können wir tippen was wir wollen und werden niemals 2 richtige haben!
Daher ist auch die untergrenze für die gewinnzahlen pro menge, wie wir es aufteilen sollten, immer gleich der gesuchten zahl an richtigen.
darum würde es auch keinen sinn machen, im sinne der informatik das 3aus3 , mit 2 hgewinnzahlen, irgendwie npchmal in 2 Mengen
P und Q zu zerlegen. dann hätte p 1 element und q 2 oder umgekehrt.
nie im leben könnte man mit elementen aus der jeweiligen gruppe 2 richtige hinkriegen, die einelementige gruppe könnte keine 2 richtige hervorbringen.
wie man das Alles mathematisch ermitteln kann?
keine Ahnung, das wüssten wir alle gern