Zackenfraktal

[efinf4]

Guten Abend

Ich habe eine Hausaufgabe für den Informatik-Unterricht und bin mir nicht ganz sicher wie das geht.




Zur Frage 1(auf dem Aufgabenblatt):

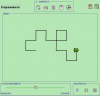
Ich muss jetzt das Fraktal bei der 4. Stufe zeichnen. Stimmt meine Lösung? Ich habe mir überlegt, dass der Winkel beim ersten Strich immer kleiner wird. Die Längen bleiben natürlich immer gleich. Stimmt das?



DAs wäre erstmal die einzige Frage, ich hoffe ihr könnt mir helfen

 

[Marco13]

Nicht so einfach wie es auf den ersten Blick aussah. Zwei Punkte, die gegen deine Lösung sprechen:
EDIT: Ach, das hast du ja: 1. Bei jeder Stufe hat sich der Winkel, in dem die Turtle lösläuft, um 45 Grad nach links verändert
2. Bei jeder Stufe hat sich die Anzahl der Schritte verdoppelt.

 

[Marco13]

Ja, hab' nochmal geschaut... Poste dann mal die Musterlösung hier. Ich würde gerne sehen, wie das aussehen soll, also wie man die Drehrichtung am Anfang und am Ende vollkommen in der Rekursion auflösen (und nicht sowas wie turtle.turn(level*45) verwenden) soll...

 

[efinf4]

Vielen Dank für Tipp, dass sich die Striche immer verdoppeln. Stimmt das so?



jetzt muss ich das ganze "nur" noch programmieren, mal schauen ob ich das schaffe.

Kannst Du mir vielleicht einen kleinen Tipp geben?

Die Vorlage müsste glaub ich so aussehen, da muss dann nur noch der restliche Code rein.

import javaturtle.JavaTurtleProgram;
        
public class Zackenfraktal extends JavaTurtleProgram {

void fraktal(int stufe, int angle)
  {
     
     if (stufe>0){
        
     }
     
  }

 public void myProgram() {
    fraktal(...,...);
  }

}

 

[Marco13]

Ich werde mich hüten, irgendwelche verbindlichen Aussagen zu "falsch oder richtig" zu machen. Alles, was ich sage ist ohne Gewähr.

Aber ich glaube, das ist falsch

Es sieht im Moment so aus, als würde es bei Zahlen >3 dann einfach weiter so im "Zickzack" laufen. Solche Rekursiven Turtleprogramme bilden aber i.a. schnell irgendwelche hübsch-chaotischen Muster.

Ehrlich gesagt fand ich es ziemlich schwer, das ganze in eine Rekursion zu packen. Insbesondere solange ich versucht hatte, die Drehung am Anfang und am Ende mit in die Rekursion zu packen. (Wenn man das NICHT versucht, ist es deutlich leichter - und von der Struktur her auch so, wie man es bei so einer Aufgabe erwarten würde).

Eigentlich kann man die erste Aufgabe nur dann sinnvoll lösen, wenn man die zweite schon gelöst hat. Und da sie auch die Voraussetzung für die dritte Aufgabe ist: Wie sieht denn deine Beschreibung der Rekursionsregel in Worten aus?

Hab' mal das angehängt, was rauskommt, wenn man ein* Programm, das für 0,1,2 und 3 die abgebildeten Ergebnisse liefert, auf die 4 losläßt. Aber nochmal: Ohne Gewähr.

* EIN Programm, weil ich nicht 100% sicher bin, ob das in irgendeiner Form eindeutig sein muss: Es gibt vielleicht(!) mehrere Programme, die für 0-3 die abgebildeten Ergebnisse liefern, sich bei 4 dann aber unterschiedlich Verhalten...

 

[XHelp]

Also ich habe genau das gleiche Ergebnis wie Marco raus. Also entweder liegen wir beide falsch, oder unsere Lösung ist richtig.
Schau einfach mal wie die Stufen 0..3 Aufgebaut sind. Vllt hilft es der Vorstellung die in der Mitte um 90 Grad zu knicken

 

[efinf4]

Insbesondere solange ich versucht hatte, die Drehung am Anfang und am Ende mit in die Rekursion zu packen. (Wenn man das NICHT versucht, ist es deutlich leichter - und von der Struktur her auch so, wie man es bei so einer Aufgabe erwarten würde).

Was heisst das? Muss man die Drehung um 45 Grad in der Mitte des Programms machen? Also zuerst um ... forward gehen dann rekursiv die stufe-1 und angle+45 oder wie?

tut mir leid, dass ich es nicht checke, aber ich bin nunmal kein Ass in Informatik

Eigentlich kann man die erste Aufgabe nur dann sinnvoll lösen, wenn man die zweite schon gelöst hat. Und da sie auch die Voraussetzung für die dritte Aufgabe ist: Wie sieht denn deine Beschreibung der Rekursionsregel in Worten aus?

Ich hab das mal so beschrieben:

Ich war gerade am überlegen wie die 4. Stufe des Zackenfraktals aussehen könnte, da sah ich, dass der Winkel vom ersten Strich immer um 45 Grad verkleinert wird. Das heißt, in der 4. Stufe musste der Anfangsstrich wieder horizontal liegen. Dann bemerkte ich, dass sich die Anzahl der Striche von Stufe zu Stufe immer verdoppelt d.h. es muss in der 4. Stufe 16 Striche geben. Die habe ich dann so angeordnet, dass der Übergang gleich war wie bei den 3 vorherigen Stufen


Ich muss die Aufgaben leider morgen schon abgeben...naja vielen Dank für die Hilfe auch wenn ichs nicht geschafft habe

 

[XHelp]

Nein, mitten im Programm muss du keine 45° Drehung machen. Schau dir die Hälfte der Stufe 3 an. Was fällt dir da auf im Bezug auf Stufe 2 auf? Und jetzt die andere im Bezug auf die links-rechts-Drehung im Vergleich zu der 1. Hälfte.

 

[Marco13]

Bei den Beispielen war die Schildkröte immer vorher und nachher in der Ausgangslage (d.h. nach rechts schauend). Ich habe keine andere Möglichkeit gefunden, das hinzukriegen, als direkt

    [b]turtle.setDirection(level*45);[/b]
    doExecute(level, 270);
    [b]turtle.setDirection(0);[/b]

auszuführen (wobei "doExecute" dann die Funktion ist, die auch rekursiv ausgerufen wird). Ich bin lange daran verzweifelt, dass ich diese Drehungen direkt in der rekursiven Funktion machen wollte (quasi ohne eine set-Methode aufzurufen). Das geht zwar insofern, dass er dann das richtige zeichnet, aber am Ende nicht nach rechts schaut....

 

[Marco13]

Es ist die Drachenkurve. Sowas aber auch.

 

[XHelp]

Bleibt nur noch der Haken mit der Drehung. Oder hast du da mitlerweile auch eine Lösung gefunden? Die Drachenkurve sieht es ja, imho, nicht vor.

 

[Marco13]

Nein, ich schätze dass man das einfach so setzen sollte, wie oben beschrieben. Das "Konzept der 'Drehung'" gibt es ja bei so einer Kurve eigentlich nicht.