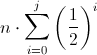Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
Laufzeitanalyse
- Themenstarter paco89
- Beginndatum
M
Marcinek
Gast
Berechne die Anzahl der Rechenoperatoren in Abhängigkeit von n.
Dann kannst du nach Komplexitätsanlyse googeln.
Siehe auch O-Notation.
Dann kannst du nach Komplexitätsanlyse googeln.
Siehe auch O-Notation.
ja, also ich hab ein wenig gegoogelt und bin wie folgt an die sache rangegangen:
zunächst einmal bezeichnet x die anzahl der operationen(unbekannter wert). außerdem habe ich die beiden verschachtelten schleifen in innere und äußere schleife unterteilt:
innere schleife:
ich rechne ja in dem schleifenrumpf der inneren schleife: 2*result *2*result * ...* und das ganze halt x-mal bis die schleifenbedingung abbricht. also lautet die ungleichung die ich aufstelle:
(2*result)^x <= 0 , da 0 die abbruchbedingung ist.
auf beiden seiten mache ich log() und daraus wird:
log((2*result)^x) <= log(0)
<=> x* log((2*result)) <= log(0)
so und ab hier habe ich ein problem, denn log(0) ist ja nicht definiert. wie muss ich weitermachen?
bei der äußeren schleife habe ich dasselbe problem:
result*result*...* <=0
<=> log(result^x) <= log(0)
<=> x*log(result) <= log(0)
hier habe ich dasselbe problem....;(
zunächst einmal bezeichnet x die anzahl der operationen(unbekannter wert). außerdem habe ich die beiden verschachtelten schleifen in innere und äußere schleife unterteilt:
innere schleife:
ich rechne ja in dem schleifenrumpf der inneren schleife: 2*result *2*result * ...* und das ganze halt x-mal bis die schleifenbedingung abbricht. also lautet die ungleichung die ich aufstelle:
(2*result)^x <= 0 , da 0 die abbruchbedingung ist.
auf beiden seiten mache ich log() und daraus wird:
log((2*result)^x) <= log(0)
<=> x* log((2*result)) <= log(0)
so und ab hier habe ich ein problem, denn log(0) ist ja nicht definiert. wie muss ich weitermachen?
bei der äußeren schleife habe ich dasselbe problem:
result*result*...* <=0
<=> log(result^x) <= log(0)
<=> x*log(result) <= log(0)
hier habe ich dasselbe problem....;(
ach so, okay...ach darauf muss ich achten, hmmh...also, dann muss ich das i nehmen, bzw. i/2 oder?
also dann würde meine rechnung lauten:
i/2 * i/2 *.... und das ganze x-mal, wobei die abbruchbedingung 0 ist, also:
(i/2)^x <=0
<=> log((i/2)^x) <= log(0)
ist das so richtig ? wenn ja, so habe ich doch wieder log(0), was ein problem darstellt, was mach ich damit?
also dann würde meine rechnung lauten:
i/2 * i/2 *.... und das ganze x-mal, wobei die abbruchbedingung 0 ist, also:
(i/2)^x <=0
<=> log((i/2)^x) <= log(0)
ist das so richtig ? wenn ja, so habe ich doch wieder log(0), was ein problem darstellt, was mach ich damit?
M
Marcinek
Gast
Tipp:
Schreibedas Programm in Java und gib für value verschiedene werte ein.
Dann siehst du wie oft die äußere Schleife in Abhängigkeit von value durchlaufen wird.
Das Ergebnis dieser überlegung muss eine Zahl sein.
Also n n² oder n³ oder oder oder
Schreibedas Programm in Java und gib für value verschiedene werte ein.
Dann siehst du wie oft die äußere Schleife in Abhängigkeit von value durchlaufen wird.
Das Ergebnis dieser überlegung muss eine Zahl sein.
Also n n² oder n³ oder oder oder
ja, die äußere wird ja so oft durchlaufen bis die schleifenbedingung nicht mehr erfüllt ist, oder wie darf ich das verstehen?
Also lautet die gesamte Antwort für deine Aufgabe: das Programm braucht so viele Schritte, wie es eben Bracht, der Wert liegt so zwischen 0 und Unendlichkeit... :bahnhof:
Anders gefragt: finde raus, wie oft
Code:
exakt
Code:
valueIch habe jetzt extra über eine Woche gewartet, da ich denke, dass die Zeit für die Hausaufgabe mittlerweile abgelaufen sein sollte.
Dennoch habe ich mich im Verlaufe des Threads gefragt, wie man denn auf die Laufzeit des Algorithmus kommt, wenn man zuerst die Laufzeit der äußeren Schleife bestimmt.
Die Laufzeit der äußeren Schleife liegt ja in O(log n) (etwas genauer wohl in floor(ld(value))+1).
Ich habe die Komplexität folgendermaßen bestimmt:
Die innere Schleife läuft i-mal durch.
i entwickelt sich wie folgt bezogen auf die äußere Schleife:
0. Durchgang: i=n
1. Durchgang: i=n*1/2
2. Durchgang: i=n*1/2*1/2
j. Durchgang: i=n*(1/2)^j
Daraus lässt sich für die ersten j Durchläufe die Reihe

aufstellen (wäre für die korrekte Aufgabenlösung mittels vollständiger Induktion zu beweisen).
Da dies eine geometrische Reihe ist, kann man den Grenzübergang wie folgt ermitteln:

Ergo liegt die Komplexität des Algorithmus in O(2n)=O(n).
Wenn man ein kleines Testprogramm schreibt, was die inneren Schleifendurchläufe zählt, dann sieht man, dass 2n tatsächlich richtig ist. Abhängig vom n liegt es teilweise auch unter 2. Je größer allerdings das n, desto besser passt die Näherung.
Um jetzt von der Komplexität der äußeren Schleife O(log n) auf O(n) zu kommen, müsste man irgendwie einen Korrekturterm bekommen (n/log n ?). Wie bekommt man den dann?
Dennoch habe ich mich im Verlaufe des Threads gefragt, wie man denn auf die Laufzeit des Algorithmus kommt, wenn man zuerst die Laufzeit der äußeren Schleife bestimmt.
Die Laufzeit der äußeren Schleife liegt ja in O(log n) (etwas genauer wohl in floor(ld(value))+1).
Ich habe die Komplexität folgendermaßen bestimmt:
Die innere Schleife läuft i-mal durch.
i entwickelt sich wie folgt bezogen auf die äußere Schleife:
0. Durchgang: i=n
1. Durchgang: i=n*1/2
2. Durchgang: i=n*1/2*1/2
j. Durchgang: i=n*(1/2)^j
Daraus lässt sich für die ersten j Durchläufe die Reihe
aufstellen (wäre für die korrekte Aufgabenlösung mittels vollständiger Induktion zu beweisen).
Da dies eine geometrische Reihe ist, kann man den Grenzübergang wie folgt ermitteln:
Ergo liegt die Komplexität des Algorithmus in O(2n)=O(n).
Wenn man ein kleines Testprogramm schreibt, was die inneren Schleifendurchläufe zählt, dann sieht man, dass 2n tatsächlich richtig ist. Abhängig vom n liegt es teilweise auch unter 2. Je größer allerdings das n, desto besser passt die Näherung.
Um jetzt von der Komplexität der äußeren Schleife O(log n) auf O(n) zu kommen, müsste man irgendwie einen Korrekturterm bekommen (n/log n ?). Wie bekommt man den dann?
Anhänge
S
SlaterB
Gast
denke nicht dass das funktionieren kann, denn die innere Schleife hat keine relativ konstante Anzahl an Schritten,
so dass man diese einfach mit der Zahl der Durchläufe multiplizieren könnte,
nur die innere Schleife betrachtet muss man n als Aufrundung annehmen, im Produkt n log(n) dann zu groß,
man weiß dass es kleiner wird, kann das aber nicht seriös ohne Betrachtung der gesamten Doppelschleife ausrechen,
wenn man aber alles betrachtet, hat man die äußere Schleife quasi und real mit drin, dann kommt man auf n auf deinen anderen Weg,
und erst dann könnte man das in das Pseudoprodukt log n * n/ log n aufteilen, helfen wird das dann aber nicht mehr
edit:
hilfreich noch dazu, denke ich:
würde i in der äußeren Schleife von 0-n durchlaufen, wäre die innere Schleife immer noch dieselbe,
das Endergebnis aber ein anderes, was sich nicht allein durch n statt log n für die äußere Schleife errechnet,
das Zusammenspiel ist wichtig, hier wäre dann die Schätzung n für die innere Schleife letzlich quasi richtig,
dennoch nicht besser als vorher
so dass man diese einfach mit der Zahl der Durchläufe multiplizieren könnte,
nur die innere Schleife betrachtet muss man n als Aufrundung annehmen, im Produkt n log(n) dann zu groß,
man weiß dass es kleiner wird, kann das aber nicht seriös ohne Betrachtung der gesamten Doppelschleife ausrechen,
wenn man aber alles betrachtet, hat man die äußere Schleife quasi und real mit drin, dann kommt man auf n auf deinen anderen Weg,
und erst dann könnte man das in das Pseudoprodukt log n * n/ log n aufteilen, helfen wird das dann aber nicht mehr
edit:
hilfreich noch dazu, denke ich:
würde i in der äußeren Schleife von 0-n durchlaufen, wäre die innere Schleife immer noch dieselbe,
das Endergebnis aber ein anderes, was sich nicht allein durch n statt log n für die äußere Schleife errechnet,
das Zusammenspiel ist wichtig, hier wäre dann die Schätzung n für die innere Schleife letzlich quasi richtig,
dennoch nicht besser als vorher
Zuletzt bearbeitet von einem Moderator:
Aktuelle Jobs
-
Wafios Softwareentwickler Cloud (JAVA/Spring) m/w/d - Reutlingen
- Gestartet von Java_Jobs
- Antworten: 0
-
Inek Senior Java Softwareentwickler (m/w/d) - Siegburg
- Gestartet von Java_Jobs
- Antworten: 0
-
Atos Senior Java Architekt (m/w/d) - Fürth
- Gestartet von Java_Jobs
- Antworten: 0
-
-
FCA Bank Java-Entwickler (m/w/d) (Heilbronn)
- Gestartet von Java_Jobs
- Antworten: 0
Neue Themen
-
Grok.Free: Your Gateway to Advanced AI Conversations Without Limits
- Gestartet von grokfree
- Antworten: 0
-
-
Softwareverifikation in der Industrie I Hat jemand irgendwelche Erfahrungen?
- Gestartet von Simon.F
- Antworten: 7
-
-