Hallo zusammen,
ich stehe mal wieder vor ein Problem womit ich es nicht programmieren kann, oder zumindest nicht schön.
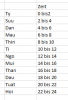
Im folgenden Bild habe ich 12 Kacheln, jede Kachelhat eine bestimmte Bezeichnung, das kommt vom chinesischen und steht jeweils für ein Tier. An sich fange ich bei Ty mit der Id und im Uhrzeigersinn wird immer um1 incrementiert. Weiter hat jede Kachel ein Monat mit sich.

Ich will über ein Algorithmus eine bestimmte Kachel finden mit folgende Angaben:
1. Geburtsmonat
2. Geburtsuhrzeit, wobei hier nur die Stunden eine Rolle spielen.
Die Kacheln habe ich jeweils in ein Enum Chi mit den Monaten gespeichert wie folgt (hellgraue Wert steht für Monate):

Beispiel: August hat den Kachel Dau.
Jetzt müsste ich noch die Geburtstuhrzeit einbeziehen und die Kacheln rückwärtslaufen
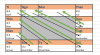
Beispiel August 14 Uhr, wenn ich auf die erste Abbildung schaue, bin ich bei Kachel Dau mit Monat August, 14 Uhr entspricht die untere Tabelle 7 Schritte zurücklaufen gegen Uhrzeigersinn, d.h. wir sind jetzt bei Mau.
Ergebnis: August 14 Uhr entsprich 1. Dau, 2. Mau

Wie würdet ihr diesen Algo entwickeln?
Ich hänge gerade bei dem zurücklaufen der Kacheln, was ist wenn das Zurücklaufen bis Ty (im Enum) geht, dann geht es mit Hoi, Tuat, Dau, etc. Ich denke Modulo ist an der Stelle richtig oder? Aber wie gehe ich da am Besten vor?
ich stehe mal wieder vor ein Problem womit ich es nicht programmieren kann, oder zumindest nicht schön.
Im folgenden Bild habe ich 12 Kacheln, jede Kachelhat eine bestimmte Bezeichnung, das kommt vom chinesischen und steht jeweils für ein Tier. An sich fange ich bei Ty mit der Id und im Uhrzeigersinn wird immer um1 incrementiert. Weiter hat jede Kachel ein Monat mit sich.

Ich will über ein Algorithmus eine bestimmte Kachel finden mit folgende Angaben:
1. Geburtsmonat
2. Geburtsuhrzeit, wobei hier nur die Stunden eine Rolle spielen.
Die Kacheln habe ich jeweils in ein Enum Chi mit den Monaten gespeichert wie folgt (hellgraue Wert steht für Monate):

Beispiel: August hat den Kachel Dau.
Jetzt müsste ich noch die Geburtstuhrzeit einbeziehen und die Kacheln rückwärtslaufen
Beispiel August 14 Uhr, wenn ich auf die erste Abbildung schaue, bin ich bei Kachel Dau mit Monat August, 14 Uhr entspricht die untere Tabelle 7 Schritte zurücklaufen gegen Uhrzeigersinn, d.h. wir sind jetzt bei Mau.
Ergebnis: August 14 Uhr entsprich 1. Dau, 2. Mau

Wie würdet ihr diesen Algo entwickeln?
Code:
public class Algo {
public static void main(String[] args) {
int birthmonth = 8;
int birthtime = 14;
for (Chi chi : Chi.values()) {
if (chi.getValue()==birthmonth) {
// an der Stelle ist es Dau
}
}
}
}Ich hänge gerade bei dem zurücklaufen der Kacheln, was ist wenn das Zurücklaufen bis Ty (im Enum) geht, dann geht es mit Hoi, Tuat, Dau, etc. Ich denke Modulo ist an der Stelle richtig oder? Aber wie gehe ich da am Besten vor?